
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A為中心將腰AB順時針旋轉90°至AE,連接DE,則△ADE的面積等于( )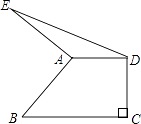
A.10
B.11
C.12
D.13
【答案】A
【解析】解:過A作AN⊥BC于N,過E作EM⊥AD,交DA延長線于M,
∵AD∥BC,∠C=90°,
∴∠C=∠ADC=∠ANC=90°,
∴四邊形ANCD是矩形,
∴∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,
∴BN=9﹣5=4,
∵∠M=∠EAB=∠MAN=∠ANB=90°,
∴∠EAM+∠BAM=90°,∠MAB+∠NAB=90°,
∴∠EAM=∠NAB,
∵在△EAM和△BAN中,  ,
,
∴△EAM≌△BAN(AAS),
∴EM=BN=4,
∴△ADE的面積是 ![]() ×AD×EM=
×AD×EM= ![]() ×5×4=10.
×5×4=10.
故選A.
過A作AN⊥BC于N,過E作EM⊥AD,交DA延長線于M,得出四邊形ANCD是矩形,推出∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,求出BN=4,求出∠EAM=∠NAB,證△EAM≌△BAN,求出EM=BN=4,根據三角形的面積公式求出即可.


科目:初中數學 來源: 題型:
【題目】如圖①是一個長為2m、寬為2n的長方形,沿圖中虛線用剪刀將其均勻分成四個小長方形,然后按圖②的形狀拼成一個正方形.
(1)你認為圖②中陰影部分的正方形的邊長等于________;
(2)請你用兩種不同的方法表示圖②中陰影部分的面積,方法一:__________________,方法二:________________;
(3)觀察圖②,你能寫出代數式(m+n)2,(m-n)2,mn之間的關系嗎?
(4)應用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點O為直線AB上一點,過O點作射線OC,使∠AOC:∠BOC=1:2,將一直角三角板的直角頂點放在點O處,一邊OM在射線OB上,另一邊ON在直線AB的下方.
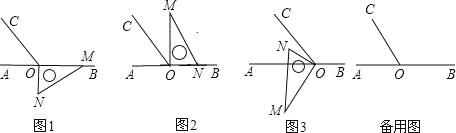
(1)將圖1中的三角板繞點O按逆時針方向旋轉至圖2的位置,使得ON落在射線OB上,此時三角板旋轉的角度為 度;
(2)繼續將圖2中的三角板繞點O按逆時針方向旋轉至圖3的位置,使得ON在∠AOC的內部.試探究∠AOM與∠NOC之間滿足什么等量關系,并說明理由;
(3)在上述直角三角板從圖1逆時針旋轉到圖3的位置的過程中,若三角板繞點O按15°每秒的速度旋轉,當直角三角板的直角邊ON所在直線恰好平分∠AOC時,求此時三角板繞點O的運動時間t的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等圓⊙O1和⊙O2相交于A、B兩點,⊙O1經過⊙O2的圓心,順次連接A、O1、B、O2 . 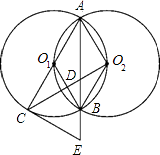
(1)求證:四邊形AO1BO2是菱形;
(2)過直徑AC的端點C作⊙O1的切線CE交AB的延長線于E,連接CO2交AE于D,求證:CE=2O2D;
(3)在(2)的條件下,若△AO2D的面積為1,求△BO2D的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】仔細閱讀下列材料.
“分數均可化為有限小數或無限循環小數”,反之,“有限小數或無限小數均可化為分數”.
例如:![]() =1÷4=0.25;
=1÷4=0.25;![]() =
=![]() =8÷5=1.6;
=8÷5=1.6;![]() =1÷3=
=1÷3=![]() ,反之,0.25=
,反之,0.25=![]() =
=![]() ;1.6=
;1.6=![]() =
=![]() =
=![]() .那么
.那么![]() ,
,![]() 怎么化成分數呢?
怎么化成分數呢?
解:∵![]() ×10=3+
×10=3+![]() , ∴不妨設
, ∴不妨設![]() =x,則上式變為10x=3+x,解得x=
=x,則上式變為10x=3+x,解得x=![]() ,即
,即![]() =
=![]() ;
;
∵![]() =
=![]() ,設
,設![]() =x,則上式變為100x=2+x,解得x=
=x,則上式變為100x=2+x,解得x=![]() ,
,
∴![]() =
=![]() =1+x=1+
=1+x=1+![]() =
=![]()
⑴將分數化為小數:![]() =______,
=______,![]() =_______;
=_______;
⑵將小數化為分數:![]() =______,
=______,![]() =_______;
=_______;
⑶將小數![]() 化為分數,需要寫出推理過程.
化為分數,需要寫出推理過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)某地區為了鼓勵市民節約用水,計劃實行生活用水按階梯式水價計費,每月用水量不超過10噸(含10噸)時,每噸按基礎價收費;每月用水量超過10噸時,超過的部分每噸按調節價收費.例如,第一個月用水16噸,需交水費17.8元,第二個月用水20噸,需交水費23元.
(1)求每噸水的基礎價和調節價;
(2)設每月用水量為n噸,應交水費為m元,寫出m與n之間的函數解析式;
(3)若某月用水12噸,應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】崇左市江州區太平鎮壺城社區調查居民雙休日的學習狀況,采取了下列調查方式;a:從崇左高中、太平鎮中、太平小學三所學校中選取200名教師;b:從不同住宅樓(即江灣花園與萬鵬住宅樓)中隨機選取200名居民;c:選取所管轄區內學校的200名在校學生.并將最合理的調查方式得到的數據制成扇形統計圖和部分數據的頻數分布直方圖.以下結論:①上述調查方式最合理的是b;②在這次調查的200名教師中,在家學習的有60人;③估計該社區2000名居民中雙休日學習時間不少于4小時的人數是1180人;④小明的叔叔住在該社區,那么雙休日他去叔叔家時,正好叔叔不學習的概率是0.1.其中正確的結論是( ) 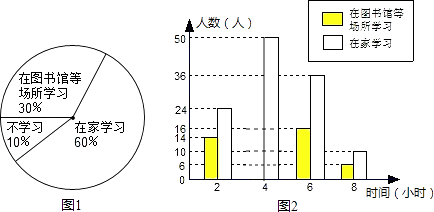
A.①④
B.②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com