
【題目】某工程,乙工程隊單獨先做10天后,再由甲、乙兩個工程隊合作20天就能完成全部工程,已知甲工程隊單獨完成此工程所需天數是乙工程隊單獨完成此工程所需天數的 ![]() ,
,
(1)求:甲、乙工程隊單獨做完成此工程各需多少天?
(2)甲工程隊每天的費用為0.67萬元,乙工程隊每天的費用為0.33萬元,該工程的預算費用為20萬元,若甲、乙工程隊一起合作完成該工程,請問工程費用是否夠用,若不夠用應追加多少萬元?
【答案】
(1)解:設乙隊單獨完成這項工程需要x天,則甲隊單獨完成這項工程需要 ![]() x天,則:
x天,則:
![]() +(
+( ![]() +
+ ![]() )×20=1,解得x=60.
)×20=1,解得x=60.
經檢驗:x=60是原方程的根,
![]() x=
x= ![]() ×60=40.
×60=40.
故甲隊單獨完成這項工程需要40天,乙隊單獨完成這項工程需要60天
(2)解:設甲、乙兩隊合作,完成這項工程需y天,則:
( ![]() +
+ ![]() )y=1,
)y=1,
解得y=24,
需要施工費用(0.67+0.33)×24=24(萬元),
24﹣20=4(萬元),
故工程費用不夠用,應追加4萬元
【解析】(1)可設乙工程隊單獨做完成此工程需x天,根據甲單獨完成這項工程所需天數是乙單獨完成這項工程所需天數的 ![]() 表示出甲工程隊單獨做完成此工程需
表示出甲工程隊單獨做完成此工程需 ![]() x天,再由乙工程隊單獨先做10天后,再由甲、乙兩個工程隊合作20天就能完成全部工程,即可得出等量關系,進而求出即可;(2)求出甲、乙兩隊施工天數得出需要施工費用,即可分析得出.
x天,再由乙工程隊單獨先做10天后,再由甲、乙兩個工程隊合作20天就能完成全部工程,即可得出等量關系,進而求出即可;(2)求出甲、乙兩隊施工天數得出需要施工費用,即可分析得出.
【考點精析】解答此題的關鍵在于理解分式方程的應用的相關知識,掌握列分式方程解應用題的步驟:審題、設未知數、找相等關系列方程、解方程并驗根、寫出答案(要有單位).


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的三個頂點的位置如圖所示,現將△ABC沿AA′的方向平移,使得點A移至圖中的點A′的位置.
(1)在直角坐標系中,畫出平移后所得△A′B′C′(其中B′、C′分別是B、C的對應點);
(2)求△ABC的面積;
(3)以A、B、C、D為頂點構造平行四邊形,則D點坐標為____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,請在下列四個關系中,選出兩個恰當的關系作為條件,推出四邊形ABCD是平行四邊形,并予以證明.(寫出一種即可)
關系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四邊形ABCD中, , ;
求證:四邊形ABCD是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九(1)班數學興趣小組經過市場調查,整理出某種商品在第x(1≤x≤90)天的售價與銷量的相關信息如下表:
時間x(天) | 1≤x<50 | 50≤x≤90 |
售價(元/件) | x+40 | 90 |
每天銷量(件) | 200﹣2x | |
已知該商品的進價為每件30元,設銷售該商品的每天利潤為y元.
(1)求出y與x的函數關系式;
(2)問銷售該商品第幾天時,當天銷售利潤最大,最大利潤是多少?
(3)該商品在銷售過程中,共有多少天每天銷售利潤不低于4800元?請直接寫出結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,且拋物線經過A(1,0),C(0,3)兩點,與x軸交于點B.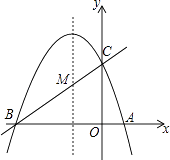
(1)若直線y=mx+n經過B、C兩點,求直線BC和拋物線的解析式;
(2)在拋物線的對稱軸x=﹣1上找一點M,使點M到點A的距離與到點C的距離之和最小,求出點M的坐標;
(3)設點P為拋物線的對稱軸x=﹣1上的一個動點,求使△BPC為直角三角形的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三位數![]() 其中a、b、c不全相等且都不為
其中a、b、c不全相等且都不為![]() ,重新排列各數位上的數字可得到一個最大數和一個最小數,此最大數和最小數的差叫做原數的差數,記為
,重新排列各數位上的數字可得到一個最大數和一個最小數,此最大數和最小數的差叫做原數的差數,記為![]() 例如,536的差數
例如,536的差數![]() .
.
(1)![]() ______,
______,![]() ______.
______.
(2)若一個三位數![]() 其中
其中![]() 且都不為
且都不為![]() ,求證:
,求證:![]() 能被99整除.
能被99整除.
(3)若s、t是各數位上的數字均不為0且互不相等兩個三位自然數,s的個位數字為1,十位數字是個位數字的3倍,百位數字為x,t的百位數字為y,十位數字是百位數字的2倍,t的個位數字與s的百位數字相同![]() ,若
,若![]() 能被3整除,
能被3整除,![]() 能被11整除,求
能被11整除,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD,點E是BC邊的中點,DE與AC相交于點F,連接BF,下列結論:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF , 其中正確的是( ) 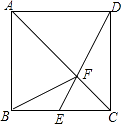
A.①③
B.②③
C.①④
D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在春節來臨之際,小楊的服裝小店用2500元購進了一批時尚圍巾,上市后很快售完,小楊又用8400元購進第二批這種圍巾,所購數量是第一批購進數量的3倍,但每條圍巾的進價多了3元.
(1)小楊兩次共購進這種圍巾多少條?
(2)如果這兩批圍巾每條的售價相同,且全部售完后總利潤率不低于20%,那么每條圍巾的售價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在安慶市第三屆中小學生道路交通安全網絡知識競賽活動中,某中學的老師要求同學們都參加社會實踐活動,一天,王明和張強兩位同學到市中心的廣場的十字路口,觀察、統計上午7:![]() :00中闖紅燈的人次,制作了如下的兩個數據統計圖
:00中闖紅燈的人次,制作了如下的兩個數據統計圖![]() 井且提出了一些問題
井且提出了一些問題
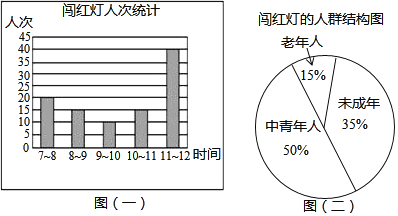
![]() 求圖
求圖![]() 一
一![]() 提供的五個數據
提供的五個數據![]() 各時段闖紅燈人次
各時段闖紅燈人次![]() 的平均數
的平均數![]() 并說明這兩幅統計圖各有什么特點?
并說明這兩幅統計圖各有什么特點?
![]() 估計一個月
估計一個月![]() 按30天計算
按30天計算![]() 上午7:
上午7:![]() :00在該十字路口闖紅燈的未成年人約有多少人次?
:00在該十字路口闖紅燈的未成年人約有多少人次?
![]() 請你根據統計圖提供的信息向交通管理部門提出一條合理化建議.
請你根據統計圖提供的信息向交通管理部門提出一條合理化建議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com