
【題目】如圖,四邊形ABCD是平行四邊形,F、G是AD邊上的兩個點,且FC平分∠BCD,GB平分∠ABC,FC與GB交于點E.
①AB=AG;②連接BF、CG,則四邊形BFGC為等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四個結論中一定成立的有( )個.

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】①∵GB平分∠ABC,
∴∠ABG=∠CBG,
在平行四邊形ABCD中,AD∥BC,
∴∠CBG=∠AGB,
∴∠ABG=∠AGB,
∴AB=AG,故本小題正確;
②假設四邊形BFGC為等腰梯形,則
BG=CF,
∴∠CBG=∠BCF,
又∵FC平分∠BCD,GB平分∠ABC,
∴∠ABC=2∠CBG,∠BCD=2∠BCF,
∴∠ABC=∠BCD,
由圖可知,平行四邊形ABCD的兩鄰角∠ABC和∠BCD不相等,故本小題錯誤;
③根據①AB=AG,
同理可得,CD=DF,
在平行四邊形ABCD中,AB=CD,
∴AG=DF,
∴AG﹣GF=DF﹣GF,
即AF=DG,故本小題正確;
④由圖可知,△ABG是鈍角三角形,△DCF是銳角三角形,
所以△ABG和△DCF形狀不同,不可能相似,故本小題錯誤,
綜上所述,正確的是①③共2個.
故選B.


科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,BP是⊙O的弦,弦CD⊥AB于點F,交BP于點G,E在CD的延長線上,EP=EG,

(1)求證:直線EP為⊙O的切線;
(2)點P在劣弧AC上運動,其他條件不變,若BG2=BFBO.試證明BG=PG;
(3)在滿足(2)的條件下,已知⊙O的半徑為3,sinB=![]() .求弦CD的長.
.求弦CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
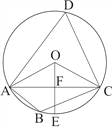
【題目】如圖,四邊形ABCD 是⊙O的內接四邊形,∠ABC=2∠D,連接OA,OC,AC
(1)求∠OCA的度數 (2)如果OE![]() AC于F,且OC=
AC于F,且OC=![]() , 求AC的長
, 求AC的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
某玩具廠生產一種玩具,按照控制固定成本降價促銷的原則,使生產的玩具能夠及時售出,據市場調查:每個玩具按![]() 元銷售時,每天可銷售
元銷售時,每天可銷售![]() 個;若銷售單價每降低元,每天可多售出
個;若銷售單價每降低元,每天可多售出![]() 個.已知每個玩具的固定成本為
個.已知每個玩具的固定成本為![]() 元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤
元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤![]() 元?
元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初二數學興趣小組活動時,碰到這樣一道題:
“已知正方形![]() ,點
,點![]() 分別在邊
分別在邊![]() 上,若
上,若![]() ,則
,則![]() ”.
”.
經過思考,大家給出了以下兩個方案:
(甲)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ;
;
(乙)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 的延長線于點
的延長線于點![]() ;同學們順利地解決了該題后,大家琢磨著想改變問題的條件,作更多的探索.
;同學們順利地解決了該題后,大家琢磨著想改變問題的條件,作更多的探索.
(1)對小杰遇到的問題,請在甲、乙兩個方案中任選一個,加以證明(如圖1);


圖1 圖2
(2)如果把條件中的“![]() ”改為“
”改為“![]() 與
與![]() 的夾角為
的夾角為![]() ”,并假設正方形
”,并假設正方形![]() 的邊長為l,
的邊長為l,![]() 的長為
的長為![]() (如圖2),試求
(如圖2),試求![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠BAE與∠BCD互為補角,AB=AE,CB=CD,連接ED,點P為ED的中點.
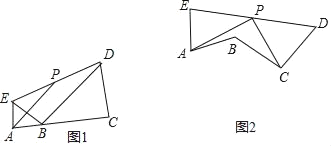
(1)如圖1,若點A,B,C三點在同一條直線上.
①求證:∠EBD=90°;②求證:AP∥BD;
(2)如圖2,若點A,B,C三點不在同一條直線上,求證:AP⊥CP.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某校田徑隊25人年齡的平均數和中位數都是16歲,但是后來發現其中有一位同學的年齡登記錯誤,將17歲寫成了19歲,經重新計算后,正確的平均數為a歲,中位數為b歲,則下列結論中正確的是( )
A. a>16,b=16 B. a>16,b<16 C. a<16,b<16 D. a<16,b=16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com