
【題目】如圖,在直角坐標系中,以點A(1,0)為圓心,以2為半徑的圓與x軸交于B,C兩點,與y軸交于D,E兩點.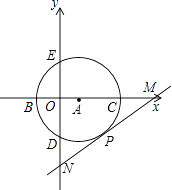
(1)直接寫出B,C,D點的坐標;
(2)若B、C、D三點在拋物線y=ax2+bx+c上,求出這個拋物線的解析式及它的頂點坐標.
(3)若圓A的切線交x軸正半軸于點M,交y軸負半軸于點N,切點為P,∠OMN=30°,試判斷直線MN是否經過B、C、D三點所在拋物線的頂點?說明理由.
【答案】
(1)
解:如圖1,連接AD,得OA=1,AD=2,

∴OD= ![]() ,
,
∴D(0,﹣ ![]() ),
),
∵點A(1,0)為圓心,以2為半徑的圓,
與x軸交于B、C兩點,
∴B(﹣1,0),C(3,0)
(2)
解:∵B(﹣1,0),C(3,0),D(0,﹣ ![]() ),
),
∴將B,C,D三點代入拋物線y=ax2+bx+c得  ,解得
,解得  ,
,
∴拋物線解析式為 ![]() ;
;
∵ ![]() ,
,
∴拋物線的頂點坐標為(1,﹣ ![]() )
)
(3)
解:如圖2,連接AP,在Rt△APM中,∠PMA=30°,AP=2,

∴AM=4,
∴M(5,0),
∵ON=MO×tan30°= ![]() ,
,
∴N(0,﹣ ![]() ),
),
設直線MN的解析式為y=kx+b,
由于點M(5,0)和N(0,﹣ ![]() )在直線MN上,則
)在直線MN上,則  ,解得
,解得  ,
,
∴直線MN的解析式為 ![]() ,
,
∵當x=1時,y=﹣ ![]() ,
,
∴點(1,﹣ ![]() )在直線
)在直線 ![]() 上,
上,
即直線MN經過拋物線的頂點
【解析】(1)連接AD,由垂徑定理可求得OD的長,可求得D點的坐標,由半徑和A點坐標可求得B、C的坐標;(2)利用待定系數法可求得拋物線解析式,化為頂點式可求得其頂點坐標;(3)連接AP,在Rt△APM中,可求得OM的長,可求得M點的坐標,從而可求得ON的長,可求得N點坐標,從而可求得直線MN的解析式,再把拋物線的頂點坐標代入進行判斷即可.
【考點精析】解答此題的關鍵在于理解一次函數的性質的相關知識,掌握一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
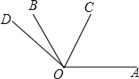
【題目】如圖,∠AOB=120°,射線OC從OA開始,繞點O逆時針旋轉,旋轉的速度為每分鐘20°;射線OD從OB開始,繞點O逆時針旋轉,旋轉的速度為每分鐘5°,OC和OD同時旋轉,設旋轉的時間為t(0≤t≤15).
(1)當t為何值時,射線OC與OD重合;
(2)當t為何值時,∠COD=90°;
(3)試探索:在射線OC與OD旋轉的過程中,是否存在某個時刻,使得射線OC,OB與OD中的某一條射線是另兩條射線所夾角的角平分線?若存在,請求出所有滿足題意的t的取值,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=6,點E為BC的中點,將△ABE沿AE折疊,使點B落在矩形內點F處,連接CF,則CF的長為( ) 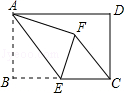
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點G,點F是CD上一點,且滿足 ![]() ,連接AF并延長交⊙O于點E,連接AD、DE,若CF=3,AF=4.
,連接AF并延長交⊙O于點E,連接AD、DE,若CF=3,AF=4. 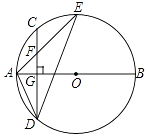
(1)求證:△ADF∽△AED;
(2)求FG的長;
(3)求tan∠E的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AB=3cm,現將紙片折疊壓平,使點A與點C重合,折痕為EF,如果sin∠BAE= ![]() ,那么重疊部分△AEF的面積為( )
,那么重疊部分△AEF的面積為( ) 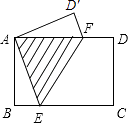
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)3![]() ﹣5
﹣5![]() ﹣(﹣1
﹣(﹣1![]() )﹣3
)﹣3![]() +12
+12![]() ﹣(﹣12
﹣(﹣12![]() )
)
(2)|﹣![]() |×[﹣32÷(﹣
|×[﹣32÷(﹣![]() )2+(﹣2)3]
)2+(﹣2)3]
(3)先化簡,再求值:2x2﹣[3(﹣![]() x2+
x2+![]() xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y滿足|x﹣
xy)﹣2y2]﹣2(x2﹣xy+2y2),其中x、y滿足|x﹣![]() |+(y+1)2=0.
|+(y+1)2=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分別是AD、CD的中點,連接BE、BF、EF.若四邊形ABCD的面積為6,則△BEF的面積為( )
,E、F分別是AD、CD的中點,連接BE、BF、EF.若四邊形ABCD的面積為6,則△BEF的面積為( ) 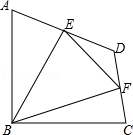
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com