Question

【題目】如圖，已知二次函數(shù)的圖象與軸交于點，點，與軸交于點．

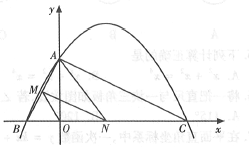
(1)求二次函數(shù)的表達(dá)式；

(2)連接，若點在線段上運動(不與點重合)，過點作，交于點，當(dāng)面積最大時，求N點的坐標(biāo)；

(3)連接，在(2)的結(jié)論下，求與的數(shù)量關(guān)系．

Answer 1

【答案】(1)；(2)N(3，0)；(3).

【解析】

試題分析：(1)把點B，C的坐標(biāo)代入到，求出a，b的值；(2)設(shè)N(n，0)，用含n的代數(shù)式表示出△ABN的面積，利用AM與AB的比，用含n的代數(shù)式表示出△AMN的面積，根據(jù)二次函數(shù)的性質(zhì)確定n的值；(3)因為點N是OC的中點，從而M是AB的中點，在直角三角形ABO中求出OM，在直角三角形AOC求出AC，即可解題．

試題解析：(1)將點B，點C的坐標(biāo)分別代入，

得：，解得：，．

∴該二次函數(shù)的表達(dá)式為．

(2)設(shè)點N的坐標(biāo)為(n，0)(－2＜n＜8)，

則，．

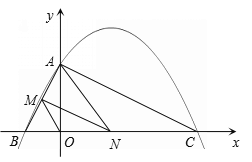
∵B(－2，0), C(8，0), ∴BC＝10.

令x＝0，解得：y＝4，

∴點A(0，4)，OA＝4，

∵MN∥AC，

∴．

∴

∴當(dāng)n＝3時，即N(3，0)時，△AMN的面積最大．

(3)當(dāng)N(3，0)時，N為BC邊中點.

∴M為AB邊中點，∴

∵，

，

∴

∴．