
【題目】如圖,正方形![]() 的頂點
的頂點![]() 、
、![]() 在圓
在圓![]() 上,若
上,若![]()
![]() ,圓
,圓![]() 的半徑為2
的半徑為2![]() ,則陰影部分的面積是__________
,則陰影部分的面積是__________![]() .(結果保留根號和
.(結果保留根號和![]() )
)

【答案】![]()
【解析】
設AD和BC分別與圓交于點E和F,連接AF、OE,過點O作OG⊥AE,根據90°的圓周角對應的弦是直徑,可得AF為圓![]() 的直徑,從而求出AF,然后根據銳角三角函數和勾股定理,即可求出∠AFB和BF,然后根據平行線的性質、銳角三角函數和圓周角定理,即可求出OG、AG和∠EOF,最后利用S陰影=S梯形AFCD-S△AOE-S扇形EOF計算即可.
的直徑,從而求出AF,然后根據銳角三角函數和勾股定理,即可求出∠AFB和BF,然后根據平行線的性質、銳角三角函數和圓周角定理,即可求出OG、AG和∠EOF,最后利用S陰影=S梯形AFCD-S△AOE-S扇形EOF計算即可.
解:設AD和BC分別與圓交于點E和F,連接AF、OE,過點O作OG⊥AE

∵四邊形ABCD是正方形
∴∠ABF=90°,AD∥BC,BC=CD=AD=![]() cm
cm
∴AF為圓![]() 的直徑
的直徑
∵![]()
![]() ,圓
,圓![]() 的半徑為2
的半徑為2![]() ,
,
∴AF=4cm
在Rt△ABF中sin∠AFB=![]() ,BF=
,BF=![]()
∴∠AFB=60°,FC=BC-BF=![]()
∴∠EAF=∠AFB=60°
∴∠EOF=2∠EAF=120°
在Rt△AOG中,OG=sin∠EAF·AO=![]() ,AG= cos∠EAF·AO=1cm
,AG= cos∠EAF·AO=1cm
根據垂徑定理,AE=2AG=2cm
∴S陰影=S梯形AFCD-S△AOE-S扇形EOF
=![]()
=![]()
=![]()
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
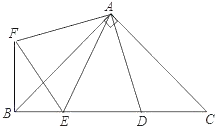
【題目】如圖,在Rt△ABC中,AB=AC,D、E是斜邊BC上的兩點,∠EAD=45°,將△ADC繞點A順時針旋轉90°,得到△AFB,連接EF.
(1)求證:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的長.
,CD=1,求FE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
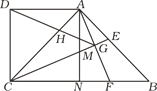
【題目】如圖,在四邊形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于點E,在BC上截取BF=AE,連接AF交CE于點G,連接DG交AC于點H,過點A作AN⊥BC,垂足為N,AN交CE于點M.則下列結論;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正確的序號是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
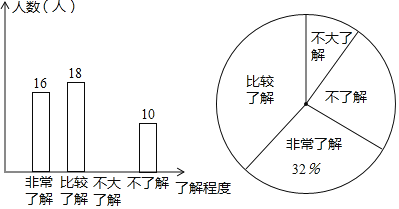
【題目】某校為了解學生對“第二十屆中國哈爾濱冰雪大世界”主題景觀的了解情況,在全體學生中隨機抽取了部分學生進行調查,并把調查結果繪制成如圖的不完整的兩幅統計圖:
(1)本次調查共抽取了多少名學生;
(2)通過計算補全條形圖;
(3)若該學校共有![]() 名學生,請你估計該學校選擇“比較了解”項目的學生有多少名?
名學生,請你估計該學校選擇“比較了解”項目的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)如圖所示,下列結論中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正確的結論有( )

A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
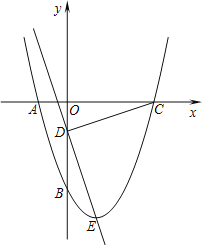
【題目】如圖所示,拋物線y=x2+bx+c經過A、B兩點,A、B兩點的坐標分別為(﹣1,0)、(0,﹣3).
(1)求拋物線的函數解析式;
(2)點E為拋物線的頂點,點C為拋物線與x軸的另一交點,點D為y軸上一點,且DC=DE,求出點D的坐標;
(3)在第二問的條件下,在直線DE上存在點P,使得以C、D、P為頂點的三角形與△DOC相似,請你直接寫出所有滿足條件的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
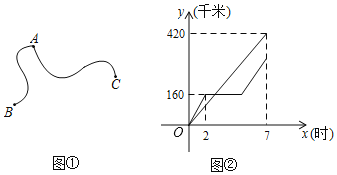
【題目】如圖①,甲、乙兩車同時從A地出發,分別勻速前往B地與C地,甲車到達B地休息一段時間后原速返回,乙車到達C地后立即返回.兩車恰好同時返回A地.圖②是兩車各自行駛的路程y(千米)與出發時間x(時)之間的函數圖象.根據圖象解答下列問題:
(1)甲車到達B地休息了 時;
(2)求甲車返回A地途中y與x之間的函數關系式;
(3)當x為何值時,兩車與A地的路程恰好相同.(不考慮兩車同在A地的情況)
查看答案和解析>>
科目:初中數學 來源: 題型:
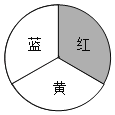
【題目】某商場開業,為了活躍氣氛,用紅、黃、藍三色均分的轉盤設計了兩種抽獎方案,凡來商場消費的顧客都可以選擇一種抽獎方案進行抽獎.
方案一:轉動轉盤一次,指針落在紅色區域可領取一份獎品;
方案二:轉動轉盤兩次,指針落在不同顏色區域可領取一份獎品,你會選擇哪個方案?請用相關的數學知識說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com