
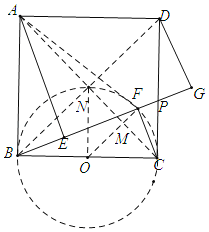
【題目】如圖,邊長為4的正方形ABCD中,點P是邊CD上一動點,作直線BP,過A、C、D三點分別作直線BP的垂線段,垂足分別是E、F、G.
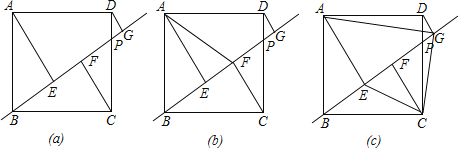
(1)如圖(a)所示,當CP=3時,求線段EG的長;
(2)如圖(b)所示,當∠PBC=30°時,四邊形ABCF的面積;
(3)如圖(c)所示,點P在CD上運動的過程中,四邊形AECG的面積S是否存在最大值?如果存在,請求出∠PBC為多少度時,S有最大值,最大值是多少?如果不存在,請說明理由.
【答案】(1)![]() ;(2)6+2
;(2)6+2![]() ;(3)當∠PBC為22.5°時,S有最大值,最大值是4+4
;(3)當∠PBC為22.5°時,S有最大值,最大值是4+4![]() .
.
【解析】
(1)延長AE交BC于點Q,過點D作DR⊥AE,由題意可證四邊形DREG是矩形,即DR=EG,由勾股定理可求BP=5,由等角的余角相等可得∠ADR=∠PBQ,可證△ADR∽△PBC,可得![]() ,可求出DR=
,可求出DR=![]() ,即EG=
,即EG=![]() ;(2)過點F作FM⊥AB于點M,作FN⊥BC于點N,由題意可證四邊形BNFM是矩形,可得FM=BN,由直角三角形的性質可求CF=2,NC=1,FN=
;(2)過點F作FM⊥AB于點M,作FN⊥BC于點N,由題意可證四邊形BNFM是矩形,可得FM=BN,由直角三角形的性質可求CF=2,NC=1,FN=![]() NC=
NC=![]() ,即FM=BN=3,根據S四邊形ABCF=S△ABF+S△BFC,可求四邊形ABCF的面積;(3)連接AF,AC,過點D作DR⊥AE,由第一問的結論和全等三角形的性質可得BF=EG,由S四邊形AECG=S△AEG+S△CEG=
,即FM=BN=3,根據S四邊形ABCF=S△ABF+S△BFC,可求四邊形ABCF的面積;(3)連接AF,AC,過點D作DR⊥AE,由第一問的結論和全等三角形的性質可得BF=EG,由S四邊形AECG=S△AEG+S△CEG=![]() ×EG×AE+
×EG×AE+![]() ×EG×CF=
×EG×CF=![]() ×BF×AE+
×BF×AE+![]() ×BF×CF=S△ABF+S△BCF=S四邊形ABCF=S△ABC+S△AFC=8+S△AFC,則當點F在AC的右側,且到AC距離最大時,S四邊形AECG值最大,由點B,點C,點F,點N四點在以O為圓心,OC為半徑的圓上,可知當OF⊥AC時,點F到AC距離最大,根據圓的有關性質和等腰三角形的性質,可求四邊形AECG的面積S是的最大值和∠PBC的度數;
×BF×CF=S△ABF+S△BCF=S四邊形ABCF=S△ABC+S△AFC=8+S△AFC,則當點F在AC的右側,且到AC距離最大時,S四邊形AECG值最大,由點B,點C,點F,點N四點在以O為圓心,OC為半徑的圓上,可知當OF⊥AC時,點F到AC距離最大,根據圓的有關性質和等腰三角形的性質,可求四邊形AECG的面積S是的最大值和∠PBC的度數;
解:
(1)如圖,延長AE交BC于點Q,過點D作DR⊥AE,
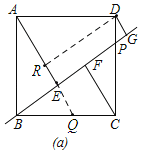
∵四邊形ABCD是正方形,
∴AD=BC=4,AD∥BC,
∴∠DAR=∠AQB,
∵∠AQB+∠PBC=90°,∠DAR+∠ADR=90°,
∴∠ADR=∠PBC,
∵PC=3,BC=4,
∴BP=![]() =5,
=5,
∵∠ADR=∠PBC,∠ARD=∠BCD=90°,
∴△ADR∽△PBC,
∴![]() ,
,
∴![]() ,
,
∴DR=![]() ,
,
∵DR⊥AE,DG⊥BP,AE⊥BP,
∴四邊形DREG是矩形,
∴EG=DR=![]() ;
;
(2)如圖,過點F作FM⊥AB于點M,作FN⊥BC于點N,
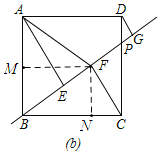
∵四邊形ABCD是正方形,
∴AB=BC=4,∠ABC=90°,
∵FM⊥AB,FN⊥BC,∠ABC=90°,
∴四邊形BNFM是矩形,
∴FM=BN,
∵∠PBC=30°,
∴FC=![]() BC=2,∠FCB=60°,
BC=2,∠FCB=60°,
∴∠NFC=30°,
∴NC=1,FN=![]() NC=
NC=![]() ,
,
∴BN=BC﹣NC=4﹣1=3=MF,
∴S四邊形ABCF=S△ABF+S△BFC,
∴S四邊形ABCF=![]() ×4×3+
×4×3+![]() ×4×
×4×![]() =6+2
=6+2![]() ;
;
(3)如圖,連接AF,AC,過點D作DR⊥AE,
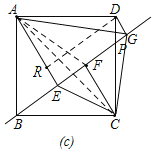
由第一問可得,DR=EG,∠ADR=∠PBC,
∵AD=BC,∠ADR=∠PBC,∠ARD=∠CFB=90°,
∴△ADR≌△CBF(AAS)
∴DR=BF,
∴BF=EG,
∵S四邊形AECG=S△AEG+S△CEG,
∴S四邊形AECG=![]() ×EG×AE+
×EG×AE+![]() ×EG×CF=
×EG×CF=![]() ×BF×AE+
×BF×AE+![]() ×BF×CF=S△ABF+S△BCF,
×BF×CF=S△ABF+S△BCF,
∴S四邊形AECG=S四邊形ABCF,
∴S四邊形AECG=S△ABC+S△AFC=8+S△AFC,
∴當點F在AC的右側,且到AC距離最大時,S四邊形AECG值最大,
如圖,連接BD交AC于點N,取BC中點O,連接ON,OF交AC于點M,
∵四邊形ABCD是正方形,
∴∠BNC=90°=∠BFC,BN=CN,
∴點B,點C,點F,點N四點在以O為圓心,OC為半徑的圓上,
∴OC=OF=ON=2,
∵BN=CN,BO=CO,∠BNC=90°,
∴∠CON=90°,∠BCN=∠CNO=45°,
∴NC=![]() ,
,
即AC=![]() ,
,
當OF⊥AC時,點F到AC的距離最大,
∵OF⊥AC,ON=OC,∠NOC=90°,
∴OM=MN=MC=![]() ,∠FOC=∠NOC=45°,
,∠FOC=∠NOC=45°,
∴FM=2﹣![]() ,
,
∴四邊形AECG的面積S的最大值=8+![]() ×4
×4![]() ×(2﹣
×(2﹣![]() )=4+4
)=4+4![]() ,
,
∵OB=OF,
∴∠PBO=∠OFB,
∵∠PBO+∠OFB=∠FOC=45°,
∴∠PBC=22.5°,
∴當∠PBC為22.5°時,S有最大值,最大值是4+4![]() .
.


科目:初中數學 來源: 題型:
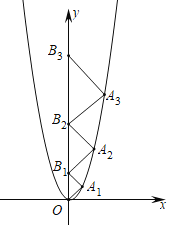
【題目】二次函數y=2x2的圖象如圖所示,坐標原點O,點B1,B2,B3在y軸的正半軸上,點A1,A2,A3在二次函數y=2x2位于第一象限的圖象上,若△A1OB1,△A2B1B2,△A3B2B3都為等腰直角三角形,且點A1,A2,A3均為直角頂點,則點A3的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,將△ABC繞頂點C逆時針旋轉得到△A′B′C,M是BC的中點,P是A′B′的中點,連接PM,若BC=2,∠BAC=30°,則線段PM的最大值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
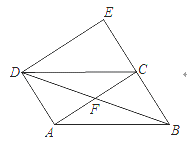
【題目】如圖,ABCD中,點E在BC延長線上,EC=BC,連接DE,AC,AC⊥AD于點A、
(1)求證:四邊形ACED是矩形;
(2)連接BD,交AC于點F.若AC=2AD,猜想∠E與∠BDE的數量關系,并證明你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綿陽某公司銷售統計了每個銷售員在某月的銷售額,繪制了如下折線統計圖和扇形統計圖: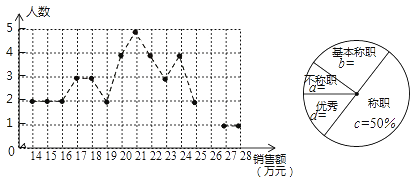
設銷售員的月銷售額為x(單位:萬元)。銷售部規定:當x<16時,為“不稱職”,當 ![]() 時為“基本稱職”,當
時為“基本稱職”,當![]() 時為“稱職”,當
時為“稱職”,當![]() 時為“優秀”.根據以上信息,解答下列問題:
時為“優秀”.根據以上信息,解答下列問題:
(1)補全折線統計圖和扇形統計圖;
(2)求所有“稱職”和“優秀”的銷售員銷售額的中位數和眾數;
(3)為了調動銷售員的積極性,銷售部決定制定一個月銷售額獎勵標準,凡月銷售額達到或超過這個標準的銷售員將獲得獎勵。如果要使得所有“稱職”和“優秀”的銷售員的一半人員能獲獎,月銷售額獎勵標準應定為多少萬元(結果去整數)?并簡述其理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】陽光市場某個體商戶購進某種電子產品,每個進價50元.調查發現,當售價為80元時,平均一周可賣出160個,而當每售價每降低2元時,平均一周可多賣出20個.若設每個電子產品降價x元,
(1)根據題意,填表:
進價(元) | 售價(元) | 每件利潤(元) | 銷量(個) | 總利潤(元) | |
降價前 | 50 | 80 | 30 | 160 |
|
降價后 | 50 | ________ | ________ | ________ | ________ |
(2)若商戶計劃每周盈利5200元,且盡量減少庫存,則每個電子產品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
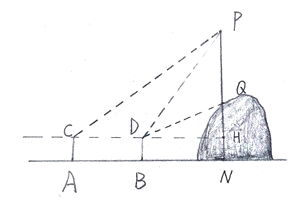
【題目】小明學校門前有座山,山上有一電線桿PQ,他很想知道電線桿PQ 的高度.于是,有一天,小明和他的同學小亮帶著側傾器和皮尺來到山腳下進行測量.測量方案如下:如圖,首先,小明站在地面上的點A處,測得電線桿頂端點P的仰角是45![]() ;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60
;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60![]() 和30
和30![]() ,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:
,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,PD切⊙O于點C,與BA的延長線交于點D,DE⊥PO交PO延長線于點E,連接PB,∠EDB=∠EPB.
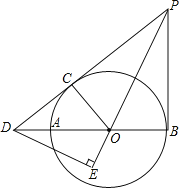
(1)求證:PB是的切線.
(2)若PB=6,DB=8,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假是旅游旺季,為吸引游客,某旅游公司推出兩條“精品路線”——“親子游”和“夏令營”。(1)7月份,“親子游”和“夏令營”活動的價格分別為8000元/人和12000元/人。其中,參加“夏令營”活動的游客人數為“親子游”活動游客人數的2倍少300人,且“夏令營”線路的旅游總收入不低于“親子游”線路旅游總收入的一半,
問:(1)參加“親子游”線路的旅游人數至少有多少人?
(2)到了8月份,該旅游公司實行降價促銷活動,“親子游”和“夏令營”線路的價格分別下降![]() 和
和![]() (
(![]() <20),旅游人數在7月份對應最小值的基礎上分別上升
<20),旅游人數在7月份對應最小值的基礎上分別上升![]() 和
和![]() ,當月旅游總收入達到256.32萬元,求
,當月旅游總收入達到256.32萬元,求![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com