
【題目】若順次連接四邊形ABCD各邊中點所得的四邊形是矩形,則下列結論中正確的是( )
A.AB∥CDB.AB⊥BCC.AC=BDD.AC⊥BD
【答案】D
【解析】
這個四邊形ABCD的對角線AC和BD的關系是互相垂直.理由為:根據題意畫出相應的圖形,如圖所示,由四邊形EFGH為矩形,根據矩形的四個角為直角得到∠FEH=90°,又EF為三角形ABD的中位線,根據中位線定理得到EF與DB平行,根據兩直線平行,同旁內角互補得到∠EMO=90°,同理根據三角形中位線定理得到EH與AC平行,再根據兩直線平行,同旁內角互補得到∠AOD=90°,根據垂直定義得到AC與BD垂直.
如圖:
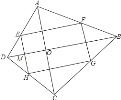
∵四邊形EFGH是矩形,
∴∠FEH=90°,
又∵點E、F、分別是AD、AB、各邊的中點,
∴EF是三角形ABD的中位線,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵點E、H分別是AD、CD各邊的中點,
∴EH是三角形ACD的中位線,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故選:D.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
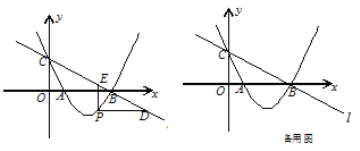
【題目】如圖,直線![]() :
: ![]() 與
與![]() 軸、
軸、![]() 軸分別交于點B、C,經過B、C兩點的拋物線
軸分別交于點B、C,經過B、C兩點的拋物線![]() 與
與![]() 軸的另一個交點為A.
軸的另一個交點為A.
(1)求該拋物線的解析式;
(2)若點P在直線![]() 下方的拋物線上,過點P作PD∥
下方的拋物線上,過點P作PD∥![]() 軸交
軸交![]() 于點D,PE∥
于點D,PE∥![]() 軸交
軸交![]() 于點E,
于點E,
求PD+PE的最大值;
(3)設F為直線![]() 上的點,以A、B、P、F為頂點的四邊形能否構成平行四邊形?若能,求出點F的坐標;若不能,請說明理由.
上的點,以A、B、P、F為頂點的四邊形能否構成平行四邊形?若能,求出點F的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年4月23日是第二十四個“世界讀書日“.某校組織讀書征文比賽活動,評選出一、二、三等獎若干名,并繪成如圖所示的條形統計圖和扇形統計圖(不完整),請你根據圖中信息解答下列問題:

(1)求本次比賽獲獎的總人數,并補全條形統計圖;
(2)求扇形統計圖中“二等獎”所對應扇形的圓心角度數;
(3)學校從甲、乙、丙、丁4位一等獎獲得者中隨機抽取2人參加“世界讀書日”宣傳活動,請用列表法或畫樹狀圖的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
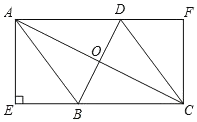
【題目】如圖,在菱形ABCD中,對角線AC,BD交于點O,AE⊥BC交CB延長線于E,CF∥AE交AD延長線于點F.
(1)求證:四邊形AECF是矩形;
(2)連接OE,若AE=8,AD=10,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為落實國務院房地產調控政策,使“居者有其屋”,某市加快了廉租房的建設力度.2015年市政府共投資3億元人民幣建設了廉租房12萬平方米,2017年計劃投資6.75億元人民幣建設廉租房,若在這兩年內每年投資的增長率相同.
(1)求每年市政府投資的增長率;
(2)若這兩年內的建設成本不變,問從2015到2017年這三年共建設了多少萬平方米廉租房?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖直線y1=﹣x+4,y2=![]() x+b都與雙曲線y=
x+b都與雙曲線y=![]() 交于點A (1,3),這兩條直線分別與x軸交于B,C兩點.
交于點A (1,3),這兩條直線分別與x軸交于B,C兩點.
(1)求k的值;
(2)直接寫出當x>0時,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列數據是甲、乙、丙三人各10輪投籃的得分(每輪投籃10次,每次投中記1分):
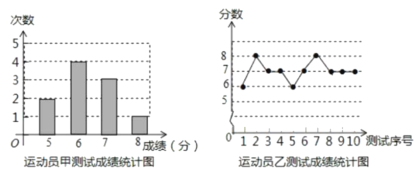
丙得分的平均數與眾數都是7,得分統計表如下:
測試序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他們三人中選擇一位投籃得分高且較為穩定的投手作為主力,你認為選誰更合適?請用你所學過的統計知識加以分析說明(參考數據:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之間進行傳球練習,每個人的球都等可能的傳給其他兩人,球最先從乙手中傳出,經過三次傳球后球又回到乙手中的概率是多少?(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖中每個小方格都是邊長為1個單位長度的正方形,![]() 在方格紙中的位置如圖所示.
在方格紙中的位置如圖所示.

(1)請在圖中建立平面直角坐標系,使得![]() ,
,![]() 兩點的坐標分別為
兩點的坐標分別為![]() ,
,![]() ,并寫出
,并寫出![]() 點的坐標;
點的坐標;
(2)在圖中作出![]() 繞坐標原點旋轉
繞坐標原點旋轉![]() 后的
后的![]() ,并寫出
,并寫出![]() ,
,![]() ,
,![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com