
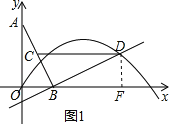
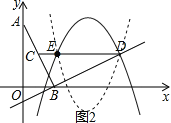
【題目】如圖,O為原點(diǎn),線段AB的兩個端點(diǎn)A(0,2),B(1,0)分別在y軸和x軸的正半軸上,點(diǎn)C為線段AB的中點(diǎn),現(xiàn)將線段BA繞點(diǎn)B按順時針方向旋轉(zhuǎn)90°得到線段BD,連結(jié)CD,某拋物線y=ax2+bx+c(a≠0)經(jīng)過點(diǎn)D、點(diǎn)E(1,1).
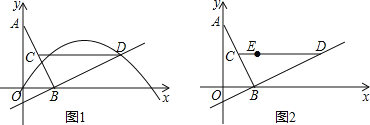
(1)若該拋物線過原點(diǎn)O,則a= ;
(2)若點(diǎn)Q在拋物線上,且滿足∠QOB與∠BCD互余,要使得符合條件的Q點(diǎn)的個數(shù)是4個,則a的取值范圍是 .
【答案】(1)﹣![]() ;(2)a<﹣
;(2)a<﹣![]() 或a>
或a>![]() .
.
【解析】
試題分析:(1)過點(diǎn)D作DF⊥x軸于點(diǎn)F,先通過三角形全等求得D的坐標(biāo),把D、E的坐標(biāo)和c=0代入y=ax2+bx+c,根據(jù)待定系數(shù)法即可求得;
(2)若符合條件的Q點(diǎn)的個數(shù)是4個,則當(dāng)a<0時,拋物線交于y軸的負(fù)半軸,當(dāng)a>0時,拋物線與直線OQ:y=﹣![]() x有兩個交點(diǎn),得到方程ax2﹣4ax+3a+1=﹣
x有兩個交點(diǎn),得到方程ax2﹣4ax+3a+1=﹣![]() x,根據(jù)根與系數(shù)的關(guān)系得出不等式,解不等式即可求得.
x,根據(jù)根與系數(shù)的關(guān)系得出不等式,解不等式即可求得.
解:(1)①過點(diǎn)D作DF⊥x軸于點(diǎn)F,如圖1,
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
在△AOB和△BFD中,
 ,
,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐標(biāo)是(3,1),
把D(3,1),E(1,1),O(0,0)代入y=ax2+bx+c,
得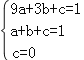 ,
,
解得a=﹣![]() ,
,
故答案為﹣![]() ;
;
(2)如圖2,∵D(3,1),E(1,1),
拋物線y=ax2+bx+c過點(diǎn)E、D,代入可得![]() ,解得
,解得![]() ,所以y=ax2﹣4ax+3a+1.
,所以y=ax2﹣4ax+3a+1.
分兩種情況:
①當(dāng)拋物線y=ax2+bx+c開口向下時,若滿足∠QOB與∠BCD互余且符合條件的Q點(diǎn)的個數(shù)是4個,則點(diǎn)Q在x軸的上、下方各有兩個.
(i)當(dāng)點(diǎn)Q在x軸的下方時,直線OQ與拋物線有兩個交點(diǎn),滿足條件的Q有2個;
(ii)當(dāng)點(diǎn)Q在x軸的上方時,要使直線OQ與拋物線y=ax2+bx+c有兩個交點(diǎn),拋物線y=ax2+bx+c與x軸的交點(diǎn)必須在x軸的正半軸上,與y軸的交點(diǎn)在y軸的負(fù)半軸,所以3a+1<0,解得a<﹣![]() ;
;
②當(dāng)拋物線y=ax2+bx+c開口向上時,點(diǎn)Q在x軸的上、下方各有兩個,
(i)當(dāng)點(diǎn)Q在x軸的上方時,直線OQ與拋物線y=ax2+bx+c有兩個交點(diǎn),符合條件的點(diǎn)Q有兩個;
(ii)當(dāng)點(diǎn)Q在x軸的下方時,要使直線OQ與拋物線y=ax2+bx+c有兩個交點(diǎn),符合條件的點(diǎn)Q才兩個.
根據(jù)(2)可知,要使得∠QOB與∠BCD互余,則必須∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO=![]() =
=![]() ,此時直線OQ的斜率為﹣
,此時直線OQ的斜率為﹣![]() ,則直線OQ的解析式為y=﹣
,則直線OQ的解析式為y=﹣![]() x,要使直線OQ與拋物線y=ax2+bx+c有兩個交點(diǎn),所以方程ax2﹣4ax+3a+1=﹣
x,要使直線OQ與拋物線y=ax2+bx+c有兩個交點(diǎn),所以方程ax2﹣4ax+3a+1=﹣![]() x有兩個不相等的實(shí)數(shù)根,所以△=(﹣4a+
x有兩個不相等的實(shí)數(shù)根,所以△=(﹣4a+![]() )2﹣4a(3a+1)>0,即4a2﹣8a+
)2﹣4a(3a+1)>0,即4a2﹣8a+![]() >0,解得a>
>0,解得a>![]() (a<
(a<![]() 舍去)
舍去)
綜上所示,a的取值范圍為a<﹣![]() 或a>
或a>![]() .
.
故答案為a<﹣![]() 或a>
或a>![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知點(diǎn)A(3,2)和點(diǎn)E是正比例函數(shù)y=ax與反比例函數(shù)![]() 的圖象的兩個交點(diǎn).
的圖象的兩個交點(diǎn).

(1)填空:點(diǎn)E坐標(biāo): ;不等式![]() 的解集為 ;
的解集為 ;
(2)求正比例函數(shù)和反比例函數(shù)的關(guān)系式;
(3)P(m,n)是函數(shù)![]() 圖象上的一個動點(diǎn),其中0<m<3.過點(diǎn)P作PB⊥y軸于點(diǎn)B,過點(diǎn)A作AC⊥x軸于點(diǎn)C,直線PB、AC交于點(diǎn)D.當(dāng)P為線段BD的中點(diǎn)時,求△POA的面積.
圖象上的一個動點(diǎn),其中0<m<3.過點(diǎn)P作PB⊥y軸于點(diǎn)B,過點(diǎn)A作AC⊥x軸于點(diǎn)C,直線PB、AC交于點(diǎn)D.當(dāng)P為線段BD的中點(diǎn)時,求△POA的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)A(![]() ,1)、B(2,0)、O(0,0),反比例函數(shù)y=
,1)、B(2,0)、O(0,0),反比例函數(shù)y=![]() 圖象經(jīng)過點(diǎn)A.
圖象經(jīng)過點(diǎn)A.
(1)求k的值;
(2)將△AOB繞點(diǎn)O逆時針旋轉(zhuǎn)60°,得到△COD,其中點(diǎn)A與點(diǎn)C對應(yīng),試判斷點(diǎn)D是否在該反比例函數(shù)的圖象上?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某政府大力扶持大學(xué)生創(chuàng)業(yè).李明在政府的扶持下投資銷售一種進(jìn)價為每件20元的護(hù)眼臺燈.物價部門規(guī)定,這種護(hù)眼臺燈的銷售單價不得高于32元.銷售過程中發(fā)現(xiàn),月銷售量y(件)與銷售單價x(元)之間的關(guān)系可近似的看作一次函數(shù):y=﹣10x+n.
(1)當(dāng)銷售單價x定為25元時,李明每月獲得利潤為w為1250元,則n= ;
(2)如果李明想要每月獲得2000元的利潤,那么銷售單價應(yīng)定為多少元?
(3)當(dāng)銷售單價定為多少元時,每月可獲得最大利潤?并求最大利潤為多少元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在同一個平面內(nèi),兩條直線的位置關(guān)系是
A. 平行或垂直 B. 相交或垂直 C. 平行或相交 D. 不能確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知AB∥x軸,A點(diǎn)的坐標(biāo)為(3,2),并且AB=5,則B點(diǎn)的坐標(biāo)為____________;
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com