
如圖,在矩形ABCD中,E是CD邊上任意一點(不與點C,D重合),作AF⊥AE交CB的延長線于點F.
(1)求證:△ADE∽△ABF;
(2)連接EF,M為EF的中點,AB=4,AD=2,設DE=x,
①求點M到FC的距離(用含x的代數式表示);
②連接BM,設 ,求y與x之間的函數關系式,并直接寫出BM的長度的最小值.
,求y與x之間的函數關系式,并直接寫出BM的長度的最小值.
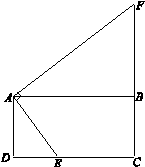
(1)證明:∵ 在矩形ABCD中,∠DAB =∠ABC =∠C =∠D =90°.
∴ 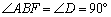 .
.
∵ AF⊥AE,
∴ ∠EAF =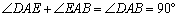 .
.
∴ 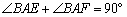 .
.
∴ ∠DAE =∠BAF.
∴ △ADE∽△ABF.
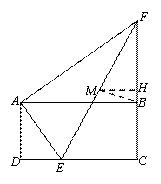 (2)解:①如圖,取FC的中點H,連接MH.
(2)解:①如圖,取FC的中點H,連接MH.
∵ M為EF的中點,
∴ MH∥DC ,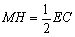 .
.
 ∵ 在矩形ABCD中,∠C =90°,
∵ 在矩形ABCD中,∠C =90°,
 ∴ MH⊥FC,即MH是點M到FC的距離.
∴ MH⊥FC,即MH是點M到FC的距離.
∵ DE=x,DC=AB=4.
∴ EC=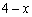 ,
,
∴ 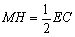
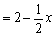 .
.
即點M到FC的距離為MH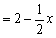 .
.
②∵△ADE∽△ABF,
∴ 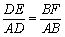 .
.
∴  .
.
∴  ,FC=
,FC=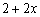 ,FH= CH=
,FH= CH= .
.
∴ 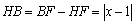 .
.
∵ 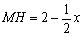 ,
,
∴ 在Rt△MHB中,
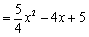 .
.
∴ 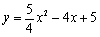 (
(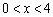 ),
),
當 時,BM長的最小值是
時,BM長的最小值是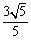 .
.


科目:初中數學 來源: 題型:
在平面直角坐標系xOy中,二次函數 的圖象與x軸負半軸交于點A,與y軸交于點B(0,4),已知點E(0,1).
的圖象與x軸負半軸交于點A,與y軸交于點B(0,4),已知點E(0,1).
(1)求m的值及點A的坐標;
(2)如圖,將△AEO沿x軸向右平移得到△A′E′O′,連結A′B、BE′.
①當點E′落在該二次函數的圖象上時,求AA′的長;
②設AA′=n,其中0<n<2,試用含n的式子表示A′B2+BE′2,并求出使 A′B2+BE′2取得最小值時點E′的坐標;
A′B2+BE′2取得最小值時點E′的坐標;
③當A′B+BE′取得最小值時,求點E′的坐標.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:二次函數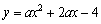
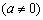 的圖象與x軸交于點A,B(A點在B點的左側),與y軸交于點C,△ABC的面積為12.
的圖象與x軸交于點A,B(A點在B點的左側),與y軸交于點C,△ABC的面積為12.
(1)①填空:二次函數圖象的對稱軸為 ;
②求二次函數的解析式;
(2) 點D的坐標為(-2,1),點P在二次函數圖象上,∠ADP為銳角,且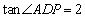 ,求點P的橫坐標;
,求點P的橫坐標;
(3)點E在x軸的正半軸上,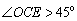 ,點O與點
,點O與點 關于EC所在直線對稱.作
關于EC所在直線對稱.作 ⊥
⊥ 于點N,交EC于點M.若EM·EC=32,求點E的坐標.
于點N,交EC于點M.若EM·EC=32,求點E的坐標.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
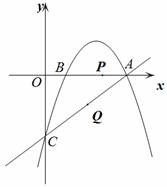
已知直線y=kx-3與x軸交于點A(4,0),與y軸交于點C,拋物線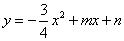 經過點A和點C,動點P在x軸上以每秒1個長度單位的速度由拋物線與x軸的另一個交點B向點A運動,點Q由點C沿線段CA向點A運動且速度是點P運動速度的2倍.
經過點A和點C,動點P在x軸上以每秒1個長度單位的速度由拋物線與x軸的另一個交點B向點A運動,點Q由點C沿線段CA向點A運動且速度是點P運動速度的2倍.
(1)求此拋物線的解析式和直線的解析式;
(2)如果點P和點Q同時出發,運動時間為t(秒),試問當t為何值時,以A、P、Q為頂點的三角形與△AOC相似;
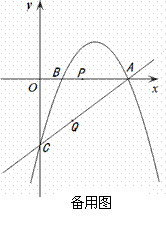 (3)在直線CA上方的拋物線上是否存在一點D,使得△ACD的面積最大.若存在,求出點D的坐標;若不存在,請說明理由.
(3)在直線CA上方的拋物線上是否存在一點D,使得△ACD的面積最大.若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,小明同學用自制的直角三角形紙板DEF測量樹的高度AB,他調整自己的位置,設法使斜邊DF保持水平,并且邊DE與點B在同一直線上.已知紙板的兩條直角邊DE=0.4m,EF=0.2cm,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹高.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com