
在平面直角坐標(biāo)系xOy中,二次函數(shù) 的圖象與x軸負(fù)半軸交于點A,與y軸交于點B(0,4),已知點E(0,1).
的圖象與x軸負(fù)半軸交于點A,與y軸交于點B(0,4),已知點E(0,1).
(1)求m的值及點A的坐標(biāo);
(2)如圖,將△AEO沿x軸向右平移得到△A′E′O′,連結(jié)A′B、BE′.
①當(dāng)點E′落在該二次函數(shù)的圖象上時,求AA′的長;
②設(shè)AA′=n,其中0<n<2,試用含n的式子表示A′B2+BE′2,并求出使 A′B2+BE′2取得最小值時點E′的坐標(biāo);
A′B2+BE′2取得最小值時點E′的坐標(biāo);
③當(dāng)A′B+BE′取得最小值時,求點E′的坐標(biāo).
 |
解:(1)由題意可知  ,
, .
.
∴ 二次函數(shù)的解析式為 .
.
∴ 點A的坐標(biāo)為(- 2, 0)
(2)①∵ 點E(0,1),由題意可知,
 .
.
解得  .
.
∴ AA′= .
.
 ②如圖,連接EE′.
②如圖,連接EE′.
由題設(shè)知AA′=n(0<n<2),則A′O = 2 - n.
在Rt△A′BO中,由A′B2 = A′O2 + BO2,
得A′B2 =(2–n)2 + 42 = n2 - 4n + 20.
∵△A′E′O′是△AEO沿x軸向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=n.
又BE=OB - OE=3.
∴在Rt△BE′E中,BE′2 = E′E2 + BE2 = n2 + 9,
∴A′B2 + BE′2 = 2n2 - 4n + 29 = 2(n–1)2 + 27.
當(dāng)n = 1時,A′B2 + BE′2可以取得最小值,此時點E′的坐標(biāo)是(1,1).
③如圖,過點A作AB′⊥x軸,并使AB′ = BE = 3.
易證△AB′A′≌△EBE′,
∴B′A′ = BE′,
∴A′B + BE′ = A′B + B′A′.
當(dāng)點B,A′,B′在同一條直線上時,A′B + B′A′最小,即此時A′B+BE′取得最小值.
易證△AB′A′∽△OBA′,
∴ ,
,
∴AA′= ,
,
∴EE′=AA′= ,
,
∴點E′的坐標(biāo)是( ,1
,1 ).
).


科目:初中數(shù)學(xué) 來源: 題型:
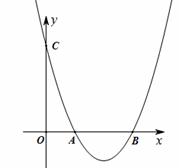
如圖 , 已知二次函數(shù)y = x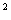 -4x + 3的圖象交x軸于A,B兩點(點A在點B的左側(cè)), 交y軸于點C.
-4x + 3的圖象交x軸于A,B兩點(點A在點B的左側(cè)), 交y軸于點C.
(1)求直線BC的解析式;
(2)點D是在直線BC下方的拋物線上的一個動點,當(dāng)△BCD的面積最大時,求D點坐標(biāo).
 解:
解:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
在一幅長8分米,寬6分米的矩形風(fēng)景畫(如圖①)的四周鑲寬度相同的金色紙邊,制成一幅矩形掛圖(如圖②).如果要使整個掛圖的面積是80平方分米,求金色紙邊的寬.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
在平面直角坐標(biāo)系 中,以點
中,以點 為圓心,4為半徑的圓與y軸所在直線的位置關(guān)系是( )
為圓心,4為半徑的圓與y軸所在直線的位置關(guān)系是( )
A.相離 B.相切 C.相交 D.無法確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
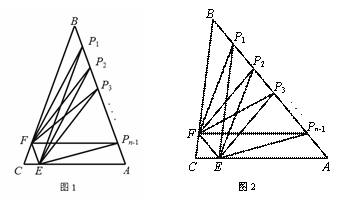
在△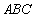 中,
中,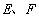 分別是
分別是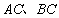 邊上的點,
邊上的點,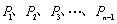 是
是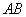 邊的
邊的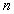 等分點,
等分點,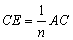 ,
,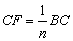 .如圖1,若
.如圖1,若 ,
,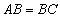 ,則∠
,則∠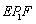 +∠
+∠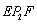 +∠
+∠ +
+  +∠
+∠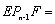 度;如圖2,若
度;如圖2,若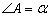 ,
,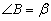 ,則∠
,則∠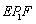 +∠
+∠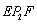 +∠
+∠ +
+  +∠
+∠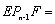 (用含
(用含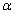 ,
, 的式子表示).
的式子表示).
 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
已知⊙O的半徑為5,點P到圓心O的距離為6,那么點P與⊙O的位置關(guān)系是
A.點P在⊙O上 B.點P在⊙O內(nèi)
C.點P在⊙O外 D.無法確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
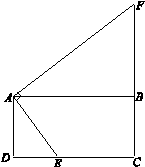
如圖,在矩形ABCD中,E是CD邊上任意一點(不與點C,D重合),作AF⊥AE交CB的延長線于點F.
(1)求證:△ADE∽△ABF;
(2)連接EF,M為EF的中點,AB=4,AD=2,設(shè)DE=x,
①求點M到FC的距離(用含x的代數(shù)式表示);
②連接BM,設(shè) ,求y與x之間的函數(shù)關(guān)系式,并直接寫出BM的長度的最小值.
,求y與x之間的函數(shù)關(guān)系式,并直接寫出BM的長度的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com