
已知:二次函數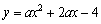
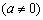 的圖象與x軸交于點A,B(A點在B點的左側),與y軸交于點C,△ABC的面積為12.
的圖象與x軸交于點A,B(A點在B點的左側),與y軸交于點C,△ABC的面積為12.
(1)①填空:二次函數圖象的對稱軸為 ;
②求二次函數的解析式;
(2) 點D的坐標為(-2,1),點P在二次函數圖象上,∠ADP為銳角,且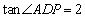 ,求點P的橫坐標;
,求點P的橫坐標;
(3)點E在x軸的正半軸上,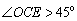 ,點O與點
,點O與點 關于EC所在直線對稱.作
關于EC所在直線對稱.作 ⊥
⊥ 于點N,交EC于點M.若EM·EC=32,求點E的坐標.
于點N,交EC于點M.若EM·EC=32,求點E的坐標.
 |
解:(1)①該二次函數圖象的對稱軸為直線 ;
;
②∵ 當x=0時,y=-4,
∴ 點C的坐標為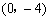 .
.
∵ 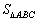

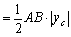 =12,
=12,
∴ AB=6.
又∵點A,B關于直線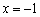 對稱,
對稱,
∴ A點和B點的坐標分別為 ,
,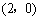 .
.
∴ 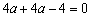 .解得
.解得 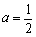 .
.
∴ 所求二次函數的解析式為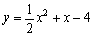 .
.
(2)如圖,作DF⊥x軸于點F.分兩種情況:
(ⅰ)當點P在直線AD的下方時,如圖所示.
由(1)得點A ,點D
,點D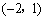 ,
,
∴ DF=1,AF=2.
在Rt△ADF中,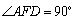 ,得
,得 .
.
延長DF與拋物線交于點P1,則P1點為所求.
∴ 點P1的坐標為 .
.
(ⅱ)當點P在直線AD的上方時,延長P1A至點G使得AG=AP1,連接DG,作GH⊥x軸于點H,如圖所示.
可證 △GHA≌△ .
.
∴ HA =AF,GH = P1 F,GA =P1A.
 又∵
又∵  ,
,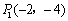 ,
,
∴ 點 的坐標是
的坐標是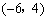 .
.
在△ADP1中,
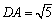 ,DP1=5,
,DP1=5,
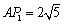 ,
,
∴  .
.
∴  .
.
∴ DA⊥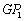 .
.
∴  .
.
∴ 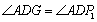 .
.
∴ 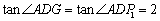 .
.
設DG與拋物線的交點為P2,則P2點為所求 .
.
作DK⊥GH于點K,作P2S∥GK交DK于點S.
設P2點的坐標為 ,
,
則 ,
,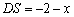 .
.
由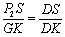 ,
, ,
,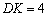 ,得
,得 .
.
整理,得 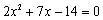 .
.
解得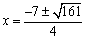 .
.
∵ P2點在第二象限,
∴ P2點的橫坐標為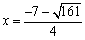 (舍正).
(舍正).
 綜上,P點的橫坐標為-2或
綜上,P點的橫坐標為-2或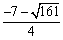 .
.
(3)如圖,連接O ,交CE于T.連接
,交CE于T.連接 C.
C.
∵ 點O與點 關于EC所在直線對稱,
關于EC所在直線對稱,
∴ O ⊥CE,
⊥CE,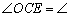
 CE,∠C
CE,∠C E
E 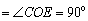 .
.
∴  C⊥
C⊥ E.
E.
∵ ON⊥ E,
E,
∴  C∥
C∥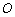 N.
N.
∴ 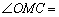
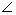
 C E
C E 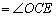 .
.
∴ 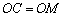 .
.
∴ 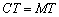 .
.
∵ 在Rt△ETO中, ,
,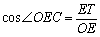 ,
,
在Rt△ 中,
中,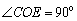 ,
, ,
,
∴ 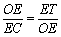 .
.
∴ 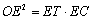

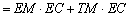
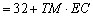 .
.
同理 
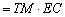
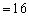 .
.
∴  .
.
∵  ,
,
∴ 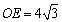 .
.
∵ 點E在x軸的正半軸上,
∴ E點的坐標為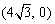 ).
).


科目:初中數學 來源: 題型:
小亮暑假期間去上海參觀世博會,決定上午從中國館(用A表示,下同)和韓國館(B)中隨機選一個館參觀,下午再從日本館(C)、非洲館(D)、法國館(E)中隨機選一個參觀,求小亮全天參觀的都是亞洲國家展館的概率是多少?(要求寫出用列表法或畫樹狀圖法求解的過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
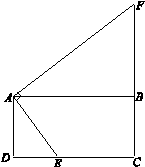
如圖,在矩形ABCD中,E是CD邊上任意一點(不與點C,D重合),作AF⊥AE交CB的延長線于點F.
(1)求證:△ADE∽△ABF;
(2)連接EF,M為EF的中點,AB=4,AD=2,設DE=x,
①求點M到FC的距離(用含x的代數式表示);
②連接BM,設 ,求y與x之間的函數關系式,并直接寫出BM的長度的最小值.
,求y與x之間的函數關系式,并直接寫出BM的長度的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
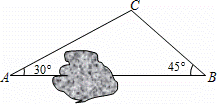
.如圖,A、B兩地之間有一座山,汽車原來從A地到B地經過C地沿折線A→C→B行駛,現(xiàn)開通隧道后,汽車直接沿直線AB行駛.已知AC=10千米,∠A=30°,∠B=45°.則隧道開通后,汽車從A地到B地比原來少走多少千米?(結果保留根號)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com