
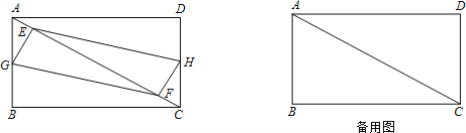
【題目】如圖,矩形ABCD中,AB=6cm,BC=8cm,E、F是對角線AC上的兩個動點(diǎn),分別從A、C同時出發(fā),相向而行,速度均為2cm/s,運(yùn)動時間為t(0≤t≤5)秒.
(1)若G、H分別是AB、DC的中點(diǎn),且t≠2.5s,求證:以E、G、F、H為頂點(diǎn)的四邊形始終是平行四邊形;
(2)在(1)的條件下,當(dāng)t為何值時?以E、G、F、H為頂點(diǎn)的四邊形是矩形;
(3)若G、H分別是折線A-B-C,C-D-A上的動點(diǎn),分別從A、C開始,與E.F相同的速度同時出發(fā),當(dāng)t為何值時,以E、G、F、H為頂點(diǎn)的四邊形是菱形,請直接寫出t的值.
【答案】(1)證明見解析;(2)當(dāng)t為4.5秒或0.5秒時,四邊形EGFH是矩形;(3)t為![]() 秒時,四邊形EGFH是菱形.
秒時,四邊形EGFH是菱形.
【解析】
(1)根據(jù)勾股定理求出AC,證明△AFG≌△CEH,根據(jù)全等三角形的性質(zhì)得到GF=HE,利用內(nèi)錯角相等得GF∥HE,根據(jù)平行四邊形的判定可得結(jié)論;
(2)如圖1,連接GH,分AC-AE-CF=8.AE+CF-AC=8兩種情況,列方程計算即可;
(3)連接AG.CH,判定四邊形AGCH是菱形,得到AG=CG,根據(jù)勾股定理求出BG,得到AB+BG的長,根據(jù)題意解答.
解:(1)∵四邊形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴∠BAC=∠DCA,
∵AB=6cm,BC=8cm,
∴AC=10cm,
∵G、H分別是AB、DC的中點(diǎn),
∴AG=![]() AB,CH=
AB,CH=![]() CD,
CD,
∴AG=CH,
∵E、F是對角線AC上的兩個動點(diǎn),分別從A、C同時出發(fā),相向而行,速度均為2cm/s,
∴AE=CF,
∴AF=CE,
∴△AGF≌△CHE(SAS),
∴GF=HE,∠AFG=∠CEH,
∴GF∥HE,
∴以E、G、F、H為頂點(diǎn)的四邊形始終是平行四邊形;
(2)如圖1,連接GH,由(1)可知四邊形EGFH是平行四邊形,
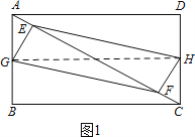
∵G、H分別是AB.DC的中點(diǎn),
∴GH=BC=8cm,
∴當(dāng)EF=GH=8cm時,四邊形EGFH是矩形,分兩種情況:
①若AE=CF=2t,則EF=10-4t=8,解得:t=0.5,
②若AE=CF=2t,則EF=2t+2t-10=8,解得:t=4.5,
即當(dāng)t為4.5秒或0.5秒時,四邊形EGFH是矩形;
(3)如圖2,連接AG、CH,
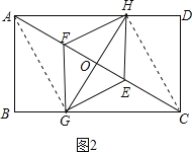
∵四邊形GEHF是菱形,
∴GH⊥EF,OG=OH,OE=OF,
∵AF=CE
∴OA=OC,
∴四邊形AGCH是菱形,
∴AG=CG,
設(shè)AG=CG=x,則BG=8-x,
由勾股定理得:AB2+BG2=AG2,
即62+(8-x)2=x2,解得:x=![]() ,
,
∴BG=8-![]() =
=![]() ,
,
∴AB+BG=6+![]() =
=![]() ,
,
t=![]() ÷2=
÷2=![]() ,
,
即t為![]() 秒時,四邊形EGFH是菱形.
秒時,四邊形EGFH是菱形.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
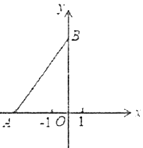
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() ,為
,為![]() 軸負(fù)半軸上一點(diǎn),點(diǎn)
軸負(fù)半軸上一點(diǎn),點(diǎn)![]() 為
為![]() 軸正半軸上一點(diǎn),其中
軸正半軸上一點(diǎn),其中![]() 滿足方程
滿足方程![]() .
.
(1)求點(diǎn)![]() 、
、![]() 的坐標(biāo);
的坐標(biāo);
(2)點(diǎn)![]() 為
為![]() 軸負(fù)半軸上一點(diǎn),且
軸負(fù)半軸上一點(diǎn),且![]() 的面積為
的面積為![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)在![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() ,使
,使![]() 的面積等于
的面積等于![]() 的面積的一半,若存在,求出相應(yīng)的
的面積的一半,若存在,求出相應(yīng)的![]() 點(diǎn)的坐標(biāo),若不存在,請說明理由.
點(diǎn)的坐標(biāo),若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,點(diǎn)M、N分別在AB、AD邊上,若AM:MB=AN:ND=1:2,則tan∠MCN=

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
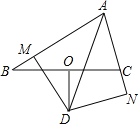
【題目】如圖,△ABC中,O是BC的中點(diǎn),D是∠BAC平分線上的一點(diǎn),且DO⊥BC,過點(diǎn)D分別作DM⊥AB于M,DN⊥AC于N.求證:BM=CN.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系上有點(diǎn)A(1,0),點(diǎn)A第一次跳動至點(diǎn)![]() ,第二次點(diǎn)
,第二次點(diǎn)![]() 跳動至點(diǎn)
跳動至點(diǎn)![]() 第三次點(diǎn)
第三次點(diǎn)![]() 跳動至點(diǎn)
跳動至點(diǎn)![]() ,第四次點(diǎn)
,第四次點(diǎn)![]() 跳動至點(diǎn)
跳動至點(diǎn)![]() ……,依此規(guī)律跳動下去,則點(diǎn)
……,依此規(guī)律跳動下去,則點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 之間的距離是( )
之間的距離是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】新華商場銷售某種冰箱,每臺進(jìn)價為2500元,銷售價為2900元,平均每天能售出8臺;調(diào)查發(fā)現(xiàn),當(dāng)銷售價每降低50元,平均每天就能多售出4臺.商場要想使這種冰箱的銷售利潤平均每天達(dá)到5000元,每臺冰箱應(yīng)該降價多少元?若設(shè)每臺冰箱降價x元,根據(jù)題意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
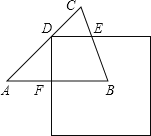
【題目】如圖,在△ABC中,AB=AC=1,∠A=45°,邊長為1的正方形的一個頂點(diǎn)D在邊AC上,與△ABC另兩邊分別交于點(diǎn)E、F,DE∥AB,將正方形平移,使點(diǎn)D保持在AC上(D不與A重合),設(shè)AF=x,正方形與△ABC重疊部分的面積為y.
(1)求y與x的函數(shù)關(guān)系式并寫出自變量x的取值范圍;
(2)x為何值時y的值最大?
(3)x在哪個范圍取值時y的值隨x的增大而減小?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=![]() AB.求證:∠B=30°.
AB.求證:∠B=30°.
請?zhí)羁胀瓿上铝凶C明.
證明:如圖,作Rt△ABC的斜邊上的中線CD,
則 CD=![]() AB=AD ( ).
AB=AD ( ).
∵AC=![]() AB,
AB,
∴AC=CD=AD 即△ACD是等邊三角形.
∴∠A= °.
∴∠B=90°﹣∠A=30°.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點(diǎn)D是AC的中點(diǎn).將一塊銳角為45°的直角三角板如圖放置,使三角板斜邊的兩個端點(diǎn)分別與A、D重合,連接BE、EC.
 試猜想線段BE和EC的數(shù)量及位置關(guān)系,并證明你的猜想.
試猜想線段BE和EC的數(shù)量及位置關(guān)系,并證明你的猜想.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com