
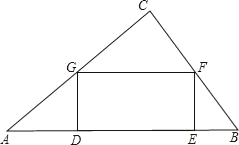
【題目】如圖,在一塊三角形區域ABC中,∠C=90°,邊AC=8m,BC=6m,現要在△ABC內建造一個矩形水池DEFG,如圖的設計方案是使DE在AB上.
(1)求△ABC中AB邊上的高h;
(2)設DG=x,當x取何值時,水池DEFG的面積(S)最大?
 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:
【題目】如圖1所示,在兩地![]() 之間有汽車站
之間有汽車站![]() 站,客車由
站,客車由![]() 地駛往
地駛往![]() 站,貨車由
站,貨車由![]() 地駛往
地駛往![]() 地兩車同時出發,勻速行駛圖2是客車、貨車離
地兩車同時出發,勻速行駛圖2是客車、貨車離![]() 站的路程
站的路程![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)之間的函數關系圖像.
(小時)之間的函數關系圖像.
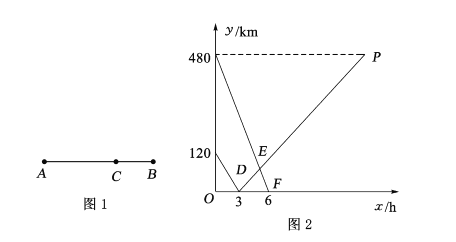
(1)填空:![]() 兩地相距 千米;貨車的速度是 千米/時;
兩地相距 千米;貨車的速度是 千米/時;
(2)求三小時后,貨車離![]() 站的路程
站的路程![]() 與行駛時間
與行駛時間![]() 之間的函數表達式;
之間的函數表達式;
(3)試求客車與貨兩車何時相距![]() 千米?
千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】本學期初,某校為迎接中華人民共和國建國七十周年,開展了以“不忘初心,緬懷革命先烈,奮斗新時代”為主題的讀書活動.校德育處對本校七年級學生四月份“閱讀該主題相關書籍的讀書量”(下面簡稱:“讀書量”)進行了隨機抽樣調查,并對所有隨機抽取學生的“讀書量”(單位:本)進行了統計,如圖所示:
所抽取該校七年級學生四月份“讀書量”的統計圖
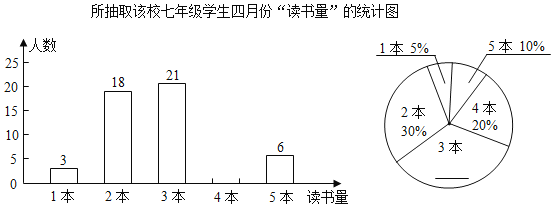
根據以上信息,解答下列問題:
(1)補全上面兩幅統計圖,填出本次所抽取學生四月份“讀書量"的眾數為____________.
(2)求本次所抽取學生四月份“讀書量"的平均數.
(3)已知該校七年級有![]() 名學生,請你估計該校七年級學生中,四月份“讀書量”為
名學生,請你估計該校七年級學生中,四月份“讀書量”為![]() 本的學生人數.
本的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2>4ac;其中正確的結論有______.(填序號)
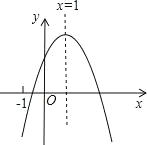
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為推進節能減排,發展低碳經濟,某市“用電大戶”用480萬元購得“變頻調速技術”后,進一步投入資金1520萬元購買配套設備,以提高用電效率達到節約用電的目的.已知該“用電大戶”生產的產品“草甘磷”每件成本費為40元.經過市場調研發現:該產品的銷售單價,需定在100元到300元之間較為合理.當銷售單價定為100元時,年銷售量為20萬件;當銷售單價超過100元,但不超過200元時,每件新產品的銷售價格每增加10元,年銷售量將減少0.8萬件;當銷售單價超過200元,但不超過300元時,每件產品的銷售價格在200元的基礎上每增加10元,年銷售量將減少1萬件.設銷售單價為x(元),年銷售量為y(萬件),年獲利為w(萬元).(年獲利=年銷售額-生產成本-節電投資)
(1)直接寫出y與x之間的函數關系式;
(2)求第一年的年獲利w與x間的函數關系式,并說明投資的第一年,該“用電大戶”是盈利還是虧損?若盈利,最大利潤是多少?若虧損,最少虧損是多少?
(3)若該“用電大戶”把“草甘磷”的銷售單價定在超過100元,但不超過200元的范圍內,并希望到第二年底,除去第一年的最大盈利(或最小虧損)后,兩年的總盈利為1842萬元,請你確定此時銷售單價.在此情況下,要使產品銷售量最大,銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
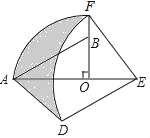
【題目】如圖,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,將Rt△AOB繞點O順時針旋轉90°后得Rt△FOE,將線段EF繞點E逆時針旋轉90°后得線段ED,分別以O,E為圓心,OA、ED長為半徑畫弧AF和弧DF,連接AD,則圖中陰影部分面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
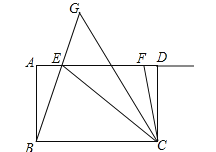
【題目】如圖,在四邊形ABCD中,AD//BC,點E在邊AD上,且CB=CE,點F是射線ED上的一個動點,![]() 的平分線CG交BE的延長線于點G.
的平分線CG交BE的延長線于點G.
(1)若![]() ,
,![]() ,求
,求![]() 的度數;
的度數;
(2)在動點F運動的過程中,![]() 的值是否發生變化?若不變,求出它的值;若變化 ,請說明理由.
的值是否發生變化?若不變,求出它的值;若變化 ,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com