【題目】在平面直角坐標系
中，拋物線
與
軸的交點為
，
(1)求拋物線的頂點坐標；
(2)若
，
①求拋物線的解析式；
②)已知點
,
，將拋物線在
的部分向上平移
個單位得到圖象
，若圖象與線段
恰有
個公共點，結合函數的圖象，直接寫出的取值范圍.
全優沖刺100分系列答案
英才點津系列答案
紅果子三級測試卷系列答案科目：初中數學 來源： 題型：
【題目】甲、乙兩組同時加工某種零件，甲組每小時加工80件，乙組加工的零件數量y（件）與時間x（小時）為一次函數關系，部分數據如下表所示．
x（小時） | 2 | 4 | 6 |
y（件） | 50 | 150 | 250 |
（1）求y與x之間的函數關系式；
（2）甲、乙兩組同時生產，加工的零件合在一起裝箱，每滿340件裝一箱，零件裝箱的時間忽略不計，求經過多長時間恰好裝滿第1箱？
查看答案和解析>>
科目：初中數學 來源： 題型：
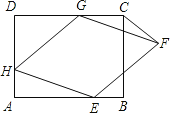
【題目】已知，如圖，矩形ABCD中，AD＝6，DC＝7，菱形EFGH的三個頂點E，G，H分別在矩形ABCD的邊AB，CD，DA上，AH＝2，連接CF．
（1）若DG＝2，求證四邊形EFGH為正方形；
（2）若DG＝6，求△FCG的面積；
（3）當DG為何值時，△FCG的面積最小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列一組方程：
；
；
；
；
它們的根有一定的規律，都是兩個連續的自然數，我們稱這類一元二次方程為“連根一元二次方程”．
若
也是“連根一元二次方程”，寫出k的值，并解這個一元二次方程；
請寫出第n個方程和它的根．
查看答案和解析>>
科目：初中數學 來源： 題型：
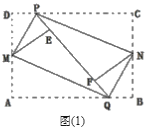
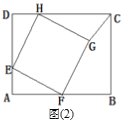
【題目】如圖，矩形紙片ABCD，DC＝8，AD＝6.
(1)如圖(1)，點E在邊AD上且AE＝2，以點E為頂點作正方形EFGH，頂點F，H分別在矩形ABCD的邊AB，CD上，連接CG，求∠HCG的度數；
(2)請從A、B兩題中任選一題解答，我選擇_____.
A.如圖(2)，甲同學把矩形紙片ABCD的四個角向內折起，恰好拼成一個無縫隙無重疊的四邊形MPNQ，判斷并說明四邊形MPNQ的形狀.
B.如圖(3)，乙同學把(1)中的“正方形EFGH”改為“菱形EFGH”，其余條件不變，此時點G落在矩形ABCD的外部，已知△CGH的面積是4，求菱形EFGH的邊長及面積.
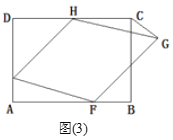
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半徑為2，圓心角為60°，則圖中陰影部分的面積是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在△ABC中，∠ABC=90°，BA=BC.將線段AB繞點A逆時針旋轉90°得到線段AD，E是邊BC上的一動點，連結DE交AC于點F，連結BF.
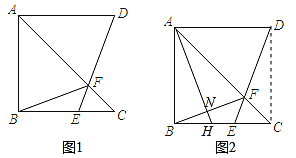
(1)求證：FB=FD；
(2)如圖2，連結CD，點H在線段BE上（不含端點），且BH=CE，連結AH交BF于點N.
①判斷AH與BF的位置關系，并證明你的結論；
②連接CN．若AB=2，請直接寫出線段CN長度的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，∠B=90°，AB=5cm，BC=7cm．點P從點A開始沿AB邊向點B以1cm/s的速度移動，點Q從點B開始沿BC邊向點C以2cm/s的速度移動．
（1）如果P，Q分別從A，B同時出發，那么幾秒后，△PBQ的面積等于6cm2？
（2）在（1）中，△PQB的面積能否等于8cm2？說明理由．
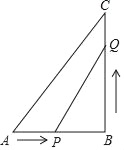
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知ABCD中，AE⊥BC于點E，以點B為中心，取旋轉角等于∠ABC，把△BAE順時針旋轉，得到△BA′E′，連接DA′．若∠ADC=60°，∠ADA′=50°，則∠DA′E′的大小為（ ）
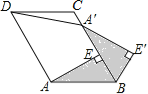
A. 130° B. 150° C. 160° D. 170°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
