
分析 根據一次函數圖象上點的坐標特征確定兩直線的交點坐標,然后根據函數圖象交點坐標為兩函數解析式組成的方程組的解選擇答案.
解答 解:把(-1,a)代入y=2x得a=-2,
則直線y=2x與y=-x+b的交點為(-1,-2),
則方程組$\left\{\begin{array}{l}{y-2x=0}\\{y+x-b=0}\end{array}\right.$的解為$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$.
故答案為:$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$.
點評 本題考查了一次函數與二元一次方程(組):函數圖象交點坐標為兩函數解析式組成的方程組的解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
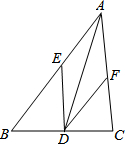 如圖,已知AD是△ABC的角平分線,DE∥AC交AB于點E,DF∥AB交AC于點F.
如圖,已知AD是△ABC的角平分線,DE∥AC交AB于點E,DF∥AB交AC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
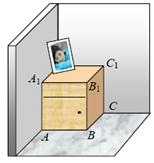 如圖,一個長方體形的木柜放在墻角處(與墻面和地面均沒有縫隙),有一只螞蟻從柜角A處沿著木柜表面爬到柜角C1處.
如圖,一個長方體形的木柜放在墻角處(與墻面和地面均沒有縫隙),有一只螞蟻從柜角A處沿著木柜表面爬到柜角C1處.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
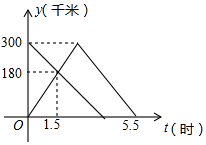 甲、乙兩車分別從A、B兩地同時出發,甲車勻速前往B地,到達B地立即以另一速度按原路勻速返回到A地;乙車勻速前往A地,設甲、乙兩車距A地的路程為y(千米),甲車行駛的時間為x(時),y與x之間的函數圖象如圖所示.
甲、乙兩車分別從A、B兩地同時出發,甲車勻速前往B地,到達B地立即以另一速度按原路勻速返回到A地;乙車勻速前往A地,設甲、乙兩車距A地的路程為y(千米),甲車行駛的時間為x(時),y與x之間的函數圖象如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com