
【題目】已知四邊形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的兩邊分別與射線CB,DC相交于點E,F,且∠EAF=60°.
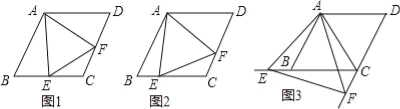
(1)如圖1,當點E是線段CB的中點時,直接寫出線段AE,EF,AF之間的數量關系;
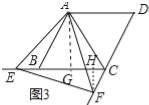
(2)如圖2,當點E是線段CB上任意一點時(點E不與B、C重合),求證:BE=CF;
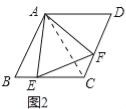
(3)如圖3,當點E在線段CB的延長線上,且∠EAB=15°時,求點F到BC的距離.
【答案】(1)AE=EF=AF;(2)證明過程見解析;(3)3-![]()
【解析】
試題分析:(1)結論AE=EF=AF.只要證明AE=AF即可證明△AEF是等邊三角形;(2)欲證明BE=CF,只要證明△BAE≌△CAF即可;(3)過點A作AG⊥BC于點G,過點F作FH⊥EC于點H,根據FH=CFcos30°,因為CF=BE,只要求出BE即可解決問題.
試題解析:(1)結論AE=EF=AF.
理由:如圖1中,連接AC, ∵四邊形ABCD是菱形,∠B=60°, ∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等邊三角形, ∴∠BAC=∠DAC=60° ∵BE=EC, ∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°, ∴∠CAF=∠DAF=30°, ∴AF⊥CD, ∴AE=AF(菱形的高相等),
∴△AEF是等邊三角形, ∴AE=EF=AF.
(2)如圖2中,∵∠BAC=∠EAF=60°, ∴∠BAE=∠CAE,
在△BAE和△CAF中,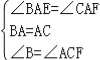 , ∴△BAE≌△CAF, ∴BE=CF.
, ∴△BAE≌△CAF, ∴BE=CF.
(3)過點A作AG⊥BC于點G,過點F作FH⊥EC于點H, ∵∠EAB=15°,∠ABC=60°, ∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4, ∴BG=2,AG=2![]() ,在RT△AEG中,∵∠AEG=∠EAG=45°,
,在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() , ∴EB=EG﹣BG=2
, ∴EB=EG﹣BG=2![]() ﹣2, ∵△AEB≌△AFC,
﹣2, ∵△AEB≌△AFC,
∴AE=AF,EB=CF=2![]() ﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等邊三角形,
﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等邊三角形,
∴∠AEF=∠AFE=60° ∵∠AEB=45°,∠AEF=60°, ∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°, ∴∠EFH=75°, ∵∠AFE=60°, ∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°, 在RT△CHF中,∵∠CFH=30°,CF=2![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2![]() ﹣2)
﹣2)![]() =3﹣
=3﹣![]() . ∴點F到BC的距離為3﹣
. ∴點F到BC的距離為3﹣![]() .
.



科目:初中數學 來源: 題型:
【題目】若M=(2015﹣1985)2,O=(2015﹣1985)×(2014﹣1986),N=(2014﹣1986)2,則M+N﹣2O的值為________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC是矩形ABCD的對角線,過AC的中點O作EF⊥AC,交BC于點E,交AD于點F,連接AE,CF.
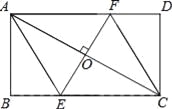
(1)求證:四邊形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區2014年投入教育經費2900萬元,2016年投入教育經費3509萬元.
(1)求2014年至2016年該地區投入教育經費的年平均增長率;
(2)按照義務教育法規定,教育經費的投入不低于國民生產總值的百分之四,結合該地區國民生產總值的增長情況,該地區到2018年需投入教育經費4250萬元,如果按(1)中教育經費投入的增長率,到2018年該地區投入的教育經費是否能達到4250萬元?請說明理由.
(參考數據: ![]() =1.1,
=1.1, ![]() =1.2,
=1.2, ![]() =1.3,
=1.3, ![]() =1.4)
=1.4)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)和正比例函數y=![]() x的圖象如圖所示,則方程ax2+(b﹣
x的圖象如圖所示,則方程ax2+(b﹣![]() )x+c=0(a≠0)的兩根之和( )
)x+c=0(a≠0)的兩根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
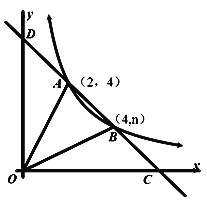
【題目】如圖,直線y=ax+b與反比例函數![]() (x>0)的圖象交于A(2,4),B(4,n)兩點,與x軸,y軸分別交于C,D兩點.
(x>0)的圖象交于A(2,4),B(4,n)兩點,與x軸,y軸分別交于C,D兩點.
(1)求m,n的值;
(2)求ΔAOB的面積
(3)若線段CD上的點P到x軸,y軸的距離相等.求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一元二次方程(x+1)(1﹣x)=2x化成二次項系數大于零的一般式為__,其中二次項系數是__,一次項系數是__,常數項是__.一元二次方程x2=2x的解為:__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學興趣小組同學想計算出學校旗桿的高度,他們發現旗桿的繩子系到地面還多1m,當繩子的下端拉開5m后,下端剛好接觸地面,則旗桿的高度是________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com