【題目】甲乙兩地相距400千米，一輛貨車和一輛轎車先后從甲地出發駛向乙地，如圖，線段OA表示貨車離甲地的路程y（千米）與所用時間x（小時）之間的函數關系，折線BCD表示轎車離甲地的路程y（千米）與x（小時）之間的函數關系，根據圖象解答下列問題：
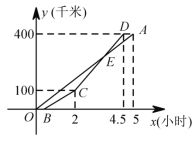
（1）求線段CD對應的函數關系式；
（2）在轎車追上貨車后到到達乙地前，何時轎車在貨車前30千米．
英才點津系列答案
紅果子三級測試卷系列答案
課堂練加測系列答案科目：初中數學 來源： 題型：
【題目】關于x的一元二次方程x2+（2k+1）x+k2+1=0有兩個不等實根
．
（1）求實數k的取值范圍．
（2）若方程兩實根滿足｜x1｜+｜x2｜=x1·x2，求k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
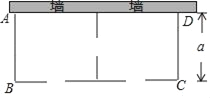
【題目】某農場要建一個飼養場（長方形ABCD），飼養場的一面靠墻（墻最大可用長度為27米），另三邊用木欄圍成，中間也用木欄隔開，分成兩個場地，并在如圖所示的三處各留1米寬的門（不用木欄），建成后木欄總長57米，設飼養場（長方形ABCD）的寬為a米．
（1）飼養場的長為多少米（用含a的代數式表示）．
（2）若飼養場的面積為288m2，求a的值．
（3）當a為何值時，飼養場的面積最大，此時飼養場達到的最大面積為多少平方米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某中學校園內有一塊長為（3a+b）米，寬為（2a+b）米的長方形地塊，學校計劃在中間留一塊邊長為（a+b）米的正方形地塊修建一座雕像，然后將陰影部分進行綠化．
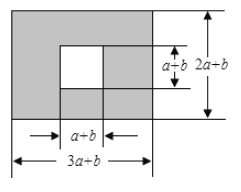
（1）求綠化的面積．（用含a、b的代數式表示）
（2）當a＝2，b＝4時，求綠化的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）教材呈現：下圖是華師版八年級上冊數學教材第94頁的部分內容．
定理證明：請根據教材中的分析，結合圖①，寫出“線段垂直平分線的性質定理”完整的證明過程．
定理應用：
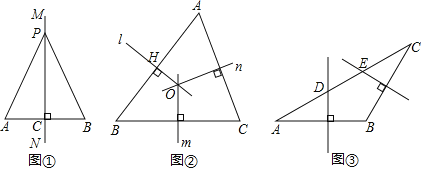
（2）如圖②，在
中，直線
、
分別是邊
、
的垂直平分線，直線、的交點為
．過點作
于點
．求證：
．
（3）如圖③，在中，
，邊
的垂直平分線
交于點
，邊的垂直平分線
交于點
．若
，
，則
的長為_____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
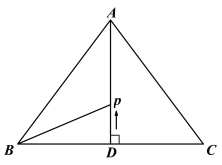
【題目】如圖，等腰三角形
中，
，
，AD為底邊BC上的高，動點
從點D出發，沿DA方向勻速運動，速度為
，運動到
點停止，設運動時間為
，連接BP．(0≤t≤8)
（1）求AD的長；
（2）設△APB的面積為y（cm），求y與t之間的函數關系式；
（3）是否存在某一時刻t，使得S△APB:S△ABC=1:3，若存在，求出
的值；若不存在，說明理由．
（4）是否存在某一時刻，使得點P在線段AB的垂直平分線上，若存在，求出的值；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
在數學課上，老師提出利用尺規作圖完成下面問題：
已知：△OAB.
求作：⊙O，使⊙O與△OAB的邊AB相切.
小明的作法如下：
如圖，①取線段OB的中點M；以M為圓心，MO為半徑作⊙M，與邊AB交于點C；
②以O為圓心，OC為半徑作⊙O；
所以，⊙O就是所求作的圓.
請回答：這樣做的依據是__________________________________________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
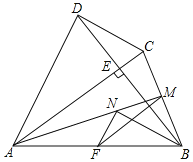
【題目】如圖，四邊形ABCD中，AC⊥BD交BD于點E，點F、M分別是AB、BC的中點，BN平分∠ABE交AM于點N，AB＝AC＝BD，連接MF，NF
求證：（1）BN＝
MN；
（2）△MFN∽△BDC．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明從家出發，外出散步，到一個公共閱報欄前看了一會報后，繼續散步了一段時間，然后回家，如圖描述了小明在散步過程匯總離家的距離s（米）與散步所用時間t（分）之間的函數關系，根據圖象，下列信息錯誤的是（ ）
A．小明看報用時8分鐘
B．公共閱報欄距小明家200米
C．小明離家最遠的距離為400米
D．小明從出發到回家共用時16分鐘
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
