
【題目】如圖,正方形ABCD的邊長為8cm,E、F、G、H分別是AB、BC、CD、DA上的動點,且AE=BF=CG=DH.
(1)求證:四邊形EFGH是正方形
(2)判斷直線EG是否經過一個定點,并說明理由
(3)求四邊形EFGH面積的最小值.
【答案】
(1)
證明:∵四邊形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,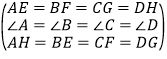 ,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四邊形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四邊形EFGH是正方形
(2)
解:直線EG經過一個定點,這個定點為正方形的中心(AC、BD的交點);理由如下:
連接AC、EG,交點為O;如圖所示:
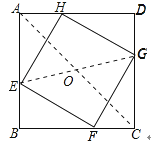
∵四邊形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,
∠OAE=∠OCG
∠AOE=∠COG
AE=CG
∴△AOE≌△COG(AAS),
∴OA=OC,即O為AC的中點,
∵正方形的對角線互相平分,
∴O為對角線AC、BD的交點,即O為正方形的中心
(3)
解:設四邊形EFGH面積為S,設BE=xcm,則BF=(8﹣x)cm,
根據勾股定理得:EF2=BE2+BF2=x2+(8﹣x)2,
∴S=x2+(8﹣x)2=2(x﹣4)2+32,
∵2>0,
∴S有最小值,
當x=4時,S的最小值=32,
∴四邊形EFGH面積的最小值為32cm2.

【解析】(1)由正方形的性質得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,證出AH=BE=CF=DG,由SAS證明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,證出四邊形EFGH是菱形,再證出∠HEF=90°,即可得出結論;
(2)連接AC、EG,交點為O;先證明△AOE≌△COG,得出OA=OC,證出O為對角線AC、BD的交點,即O為正方形的中心;
(3)設四邊形EFGH面積為S,BE=xcm,則BF=(8﹣x)cm,由勾股定理得出S=x2+(8﹣x)2=2(x﹣4)2+32,S是x的二次函數,容易得出四邊形EFGH面積的最小值.


 互動英語系列答案
互動英語系列答案科目:初中數學 來源: 題型:
【題目】某商場統計了今年1~5月A,B兩種品牌冰箱的銷售情況,并將獲得的數據繪制成折線統計圖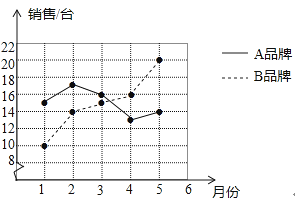
(1)分別求該商場這段時間內A,B兩種品牌冰箱月銷售量的中位數和方差。
(2)根據計算結果,比較該商場1~5月這兩種品牌冰箱月銷售量的穩定性。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A,B的坐標分別為(﹣3,0),(3,0),點P在反比例函數y=![]() 的圖象上,若△PAB為直角三角形,則滿足條件的點P的個數為( )
的圖象上,若△PAB為直角三角形,則滿足條件的點P的個數為( )
A.2個
B.4個
C.5個
D.6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區教研部門對本區初二年級的學生進行了一次隨機抽樣問卷調查,其中有這樣一個問題:
老師在課堂上放手讓學生提問和表達,
A.從不 B.很少 C.有時 D.常常 E.總是
答題的學生在這五個選項中只能選擇一項.如圖是根據學生對該問題的答卷情況繪制的兩幅不完整的統計圖.
根據以上信息,解答下列問題:
(1)該區共有 名初二年級的學生參加了本次問卷調查
(2)請把這幅條形統計圖補充完整
(3)在扇形統計圖中,“總是”所占的百分比為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的半徑為2,△ABC是⊙O的內接三角形,連接OB、OC.若∠BAC與∠BOC互補,則弦BC的長為( ) 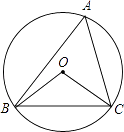
A.4 ![]()
B.3 ![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD內接于⊙O,如圖所示,在劣弧 ![]() 上取一點E,連接DE、BE,過點D作DF∥BE交⊙O于點F,連接BF、AF,且AF與DE相交于點G,求證:
上取一點E,連接DE、BE,過點D作DF∥BE交⊙O于點F,連接BF、AF,且AF與DE相交于點G,求證: 
(1)四邊形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2﹣2x+3 的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C
(1)求A、B、C的坐標;
(2)過拋物線上一點F作y軸的平行線,與直線AC交于點G.若FG= ![]() AC,求點F的坐標;
AC,求點F的坐標;
(3)E(0,﹣2),連接BE.將△OBE繞平面內的某點逆時針旋轉90°得到△O′B′E′,O、B、E的對應點分別為O′、B′、E′.若點B′、E′兩點恰好落在拋物線上,求點B′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,頂點為M的拋物線y=a(x+1)2﹣4分別與x軸相交于點A,B(點A在點B的右側),與y軸相交于點C(0,﹣3).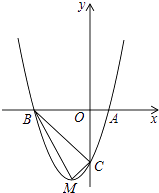
(1)求拋物線的函數表達式;
(2)判斷△BCM是否為直角三角形,并說明理由.
(3)拋物線上是否存在點N(點N與點M不重合),使得以點A,B,C,N為頂點的四邊形的面積與四邊形ABMC的面積相等?若存在,求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com