
【題目】如圖,AB是半圓O的直徑,AB=a,C是半圓上一點,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,連接CD,DB,OD.
(1)求證:△CDF≌△BDE;
(2)當AD= 時,四邊形AODC是菱形;
(3)當AD= 時,四邊形AEDF是正方形.

【答案】(1)證明見解析(2)四邊形AODC是菱形(3)OD⊥AB
【解析】
試題分析:(1)根據角平分線的性質,可得DF與DE的關系,根據圓周角定理,可得DC與DB的關系,根據HL,可得答案;
(2)根據菱形的性質,可得OD與CD,OD與BD的關系,根據正三角形的性質,可得∠DBA的度數,根據三角函數值,可得答案;
(3)根據圓周角定理,可得OD⊥AB,根據勾股定理,可得答案.
試題解析:(1)證明:∵弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
∵弦AD平分∠BAC,
∴∠FAD=∠BAD,
∴BD=CD.
在Rt△BED和Rt△CFD中![]() ,
,
∴Rt△BED≌Rt△CFD (HL);
(2)四邊形AODC是菱形時,
OD=CD=DB=OB,
∴∠DBA=60°,
∴AD=ABcos∠DBA=asin60°=![]() a,
a,
(3)當OD⊥AB,即OD與OE重合時,四邊形AEDF是正方形,
由勾股定理,得
AD=![]() ,
,


科目:初中數學 來源: 題型:
【題目】如圖所示,已知AB∥CD,分別探究下面圖形中∠APC,∠PAB,∠PCD的關系,請你從四個圖形中任選一個,說明你所探究的結論的正確性.
①結論:(1)
(2)
(3)
(4)
②選擇結論 (1) , 說明理由.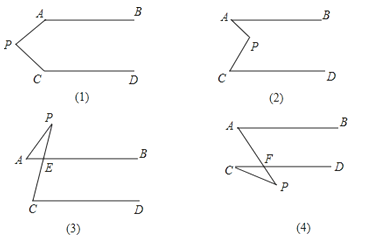
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗中學為了鼓勵同學們參加體育鍛煉,決定為每個班級配備排球或足球一個,已知一個排球和兩個足球需要140元,兩個排球和一個足球需要230元.
(1)求排球和足球的單價.
(2)全校共有50個班,學校準備拿出不超過2400元購買這批排球和足球,并且要保證排球的數量不超過足球數量的![]() ,問:學校共有幾種購買方案?哪種購買方案總費用最低?
,問:學校共有幾種購買方案?哪種購買方案總費用最低?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知平面內有兩條直線AB、CD,且AB∥CD,P為一動點.
(1)當點P移動到AB、CD之間時,如圖(1),這時∠P與∠A、∠C有怎樣的關系?證明你的結論.
(2)當點P移動到如圖(2)的位置時,∠P與∠A、∠C又有怎樣的關系?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義新運算:對于任意實數a,b,都有a⊕b=a(a﹣b)+1,等式右邊是通常的加法,減法及乘法運算.
比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范圍,并在數軸上表示出來.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com