
【題目】對于平面直角坐標系xOy中的定點P和圖形F,給出如下定義:若在圖形F上存在一點N,使得點Q,點P關于直線ON對稱,則稱點Q是點P關于圖形F的定向對稱點.
(1)如圖,![]() ,
,![]() ,
,![]() ,
,

①點P關于點B的定向對稱點的坐標是 ;
②在點![]() ,
,![]() ,
,![]() 中,______是點P關于線段AB的定向對稱點.
中,______是點P關于線段AB的定向對稱點.
(2)直線![]() 分別與x軸,y軸交于點G,H,⊙M是以點
分別與x軸,y軸交于點G,H,⊙M是以點![]() 為圓心,
為圓心,![]() 為半徑的圓.
為半徑的圓.
①當![]() 時,若⊙M上存在點K,使得它關于線段GH的定向對稱點在線段GH上,求
時,若⊙M上存在點K,使得它關于線段GH的定向對稱點在線段GH上,求![]() 的取值范圍;
的取值范圍;
②對于![]() ,當
,當![]() 時,若線段GH上存在點J,使得它關于⊙M的定向對稱點在⊙M上,直接寫出b的取值范圍.
時,若線段GH上存在點J,使得它關于⊙M的定向對稱點在⊙M上,直接寫出b的取值范圍.
【答案】(1)①![]() ;②點C,D;(2)①
;②點C,D;(2)①![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)①求出點P關于直線OB的對稱點G即可.
②求出OP,OC,OD,OE的長即可判斷.
(2)①求出兩種特殊位置b的值即可.如圖2中,作⊙M關于y軸的對稱圖形⊙M′,當直線GH與⊙M′在第一象限相切時,設切點為P,連接PM′.如圖3中,以O為圓心,3為半徑作⊙O,當直線GH與⊙O在第四象限點相切于點P時,連接OP,分別求出OH的值即可解決問題.
②如圖4中,設⊙M交x軸于K,T,則K(﹣1,0),T(5,0).求出兩種特殊位置b的值即可判斷.
解:(1)①如圖1中,
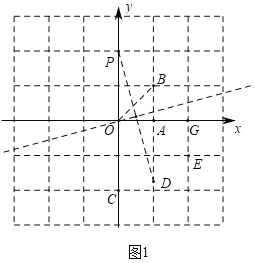
∵P(0,2),B(1,1),
∴點P關于OB的對稱點G(2,0),
故答案為:(2,0).
②∵點C(0,﹣2),D(1,﹣![]() ),E(2,﹣1),
),E(2,﹣1),
∴OP=2,OD=2,OC=2,OE=![]() ,
,
∴OP=OD=OC,
∴點C,D是點P關于線段AB的定向對稱點.
故答案為:點C,D.
(2)①如圖2中,作⊙M關于y軸的對稱圖形⊙M′,當直線GH與⊙M′在第一象限相切時,設切點為P,連接PM′,
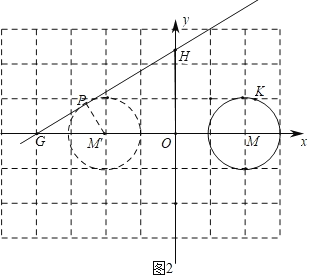
當b>0時,
由題意得:tan∠HGO=![]() ,
,
∴∠PGM=30°,
∵PM′=1,∠MPG=90°,
∴MG=2MP=2,
∴OG=GM+OM=4,
∴OH=OGtan30°=![]() ,
,
當直線經過(-1,0)時,![]() .
.
∴![]()
若b<0時,
當當直線經過(1,0)時,![]() .
.
如圖3中,以O為圓心,3為半徑作⊙O,當直線GH與⊙O在第四象限點相切于點P時,連接OP,
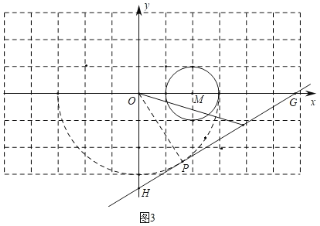
同法可得OH=2![]() ,∴
,∴![]()
觀察圖象可知滿足條件的b的值:﹣2![]() ≤b≤
≤b≤![]() .
.
綜上所述,b的取值范圍是![]() 或
或![]() .
.
②如圖4中,設⊙M交x軸于K,T,則K(﹣1,0),T(5,0).
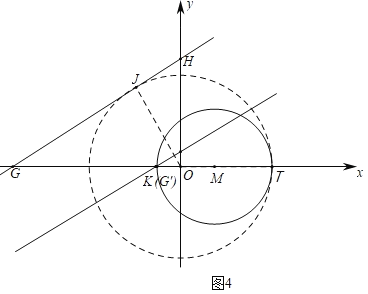
以O為圓心,5為半徑作⊙O,當直線GH與⊙O在第二象限相切于點J時,
可得OH= ,
,
此時直線GH的解析式為y=![]() x+
x+![]() ,
,
當直線GH經過點K(﹣1,0)時,0=﹣![]() +b,
+b,
可得b=![]() ,
,
此時直線GH的解析式為y=![]() x+
x+![]() ,
,
觀察圖象可知滿足條件的b的值為:![]() ≤b≤
≤b≤![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
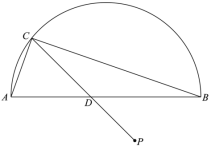
【題目】如圖,![]() 是半圓的直徑,P是半圓與直徑
是半圓的直徑,P是半圓與直徑![]() 所圍成的圖形的外部的一定點,D是直徑
所圍成的圖形的外部的一定點,D是直徑![]() 上一動點,連接
上一動點,連接![]() 并延長,交半圓于點C,連接
并延長,交半圓于點C,連接![]() .已知
.已知![]() ,設
,設![]() 兩點間的距離為
兩點間的距離為![]() ,
,![]() 兩點之間的距離為
兩點之間的距離為![]() 兩點之間的距離為
兩點之間的距離為![]() .
.
小明根據學習函數的經驗,分別對函數![]() 隨自變量x的變化而變化的規律進行了探究.
隨自變量x的變化而變化的規律進行了探究.
下面是小明的探究過程,請補充完整:
(1)按照下表自變量x的值進行取點、畫圖、測量,分別得到![]() 與x的幾組對應值;
與x的幾組對應值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點
中,描出補全后的表中各組數值所對應的點![]() ,
,![]() ,并畫出函數
,并畫出函數![]() 的圖象;
的圖象;
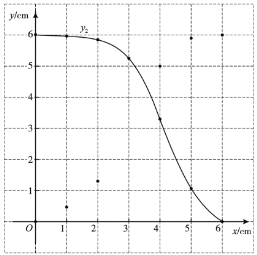
(3)結合函數圖象,解決問題:當![]() 有一個角的正弦值為
有一個角的正弦值為![]() 時,
時,![]() 的長約為_____cm.
的長約為_____cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某扶貧工作隊為一貧困戶提供了![]() 萬元的無息脫貧貸款.該貧困戶利用這筆貸款,注冊了一家網店,銷售一種成本價為
萬元的無息脫貧貸款.該貧困戶利用這筆貸款,注冊了一家網店,銷售一種成本價為![]() 元/件的農產品.已知銷售價高于成本價,且不高于
元/件的農產品.已知銷售價高于成本價,且不高于![]() 元/件,網店每月需支付電費等其它費用
元/件,網店每月需支付電費等其它費用![]() 千元市場調查發現,該農產品每月銷售量為
千元市場調查發現,該農產品每月銷售量為![]() (百件)與銷售價
(百件)與銷售價![]() (元/件)之間的函數關系如圖所示
(元/件)之間的函數關系如圖所示
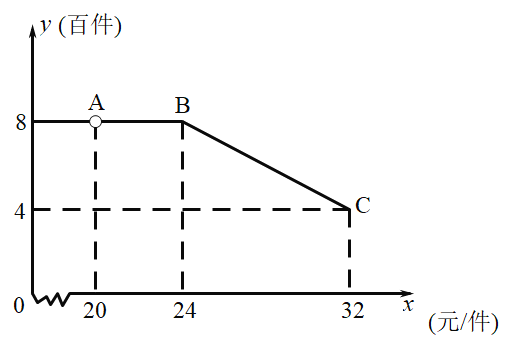
(1)求該網店每月利潤![]() (百元)與銷售價
(百元)與銷售價![]() (元/件)之間的函數關系式,并注明自變量
(元/件)之間的函數關系式,并注明自變量![]() 的取值范圍:
的取值范圍:
(2)該貧困戶從網店開業起,最快在第幾個月可用銷售利潤還清無息貸款?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸的負半軸交于點
軸的負半軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,連結
,連結![]() ,點C(6,
,點C(6,![]() )在拋物線上,直線
)在拋物線上,直線![]() 與
與![]() 軸交于點
軸交于點![]()
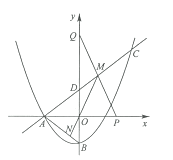
(1)求![]() 的值及直線
的值及直線![]() 的函數表達式;
的函數表達式;
(2)點![]() 在
在![]() 軸正半軸上,點
軸正半軸上,點![]() 在
在![]() 軸正半軸上,連結
軸正半軸上,連結![]() 與直線
與直線![]() 交于點
交于點![]() ,連結
,連結![]() 并延長交
并延長交![]() 于點
于點![]() ,若
,若![]() 為
為![]() 的中點.
的中點.
①求證:![]() ;
;
②設點![]() 的橫坐標為
的橫坐標為![]() ,求
,求![]() 的長(用含
的長(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C,D是⊙O上兩點,且![]() ,連接OC,BD,OD.
,連接OC,BD,OD.
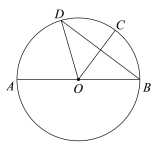
(1)求證:OC垂直平分BD;
(2)過點C作⊙O的切線交AB的延長線于點E,連接AD,CD.
①依題意補全圖形;
②若AD=6,![]() ,求CD的長.
,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB = 90,D為AB的中點,AE∥DC,CE∥DA.
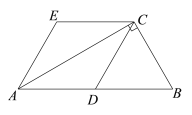
(1)求證:四邊形ADCE是菱形;
(2)連接DE,若AC =![]() ,BC =2,求證:△ADE是等邊三角形.
,BC =2,求證:△ADE是等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系xOy中的定點P和圖形F,給出如下定義:若在圖形F上存在一點N,使得點Q,點P關于直線ON對稱,則稱點Q是點P關于圖形F的定向對稱點.
(1)如圖,![]() ,
,![]() ,
,![]() ,
,

①點P關于點B的定向對稱點的坐標是 ;
②在點![]() ,
,![]() ,
,![]() 中,______是點P關于線段AB的定向對稱點.
中,______是點P關于線段AB的定向對稱點.
(2)直線![]() 分別與x軸,y軸交于點G,H,⊙M是以點
分別與x軸,y軸交于點G,H,⊙M是以點![]() 為圓心,
為圓心,![]() 為半徑的圓.
為半徑的圓.
①當![]() 時,若⊙M上存在點K,使得它關于線段GH的定向對稱點在線段GH上,求
時,若⊙M上存在點K,使得它關于線段GH的定向對稱點在線段GH上,求![]() 的取值范圍;
的取值范圍;
②對于![]() ,當
,當![]() 時,若線段GH上存在點J,使得它關于⊙M的定向對稱點在⊙M上,直接寫出b的取值范圍.
時,若線段GH上存在點J,使得它關于⊙M的定向對稱點在⊙M上,直接寫出b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電器商場銷售每臺進價分別為200元、170元的A、B兩種型號的電風扇,下表是該型號電風扇近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 3臺 | 5臺 | 1800元 |
第二周 | 4臺 | 10臺 | 3100元 |
![]() 求A、B兩種型號的電風扇的銷售單價;
求A、B兩種型號的電風扇的銷售單價;
![]() 若該商場準備用不多于5400元的金額再采購這兩種型號的電風扇共30臺,假設售價不變,那么商場應采用哪種采購方案,才能使得當銷售完這些風扇后,商場獲利最多?最多可獲利多少元?
若該商場準備用不多于5400元的金額再采購這兩種型號的電風扇共30臺,假設售價不變,那么商場應采用哪種采購方案,才能使得當銷售完這些風扇后,商場獲利最多?最多可獲利多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com