
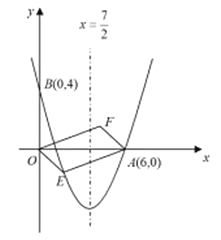
【題目】如圖,對稱軸為直線![]() 的拋物線經過點
的拋物線經過點![]() 和
和![]() .
.
(1)求拋物線解析式;
(2)設點![]() 是拋物線上一動點,且位于第四象限,四邊形
是拋物線上一動點,且位于第四象限,四邊形![]() 是以
是以![]() 為對角線的平行四邊形.
為對角線的平行四邊形.
①求平行四邊形![]() 的面積
的面積![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
②當平行四邊形![]() 的面積為24時,請判斷平行四邊形
的面積為24時,請判斷平行四邊形![]() 是否為菱形?
是否為菱形?
③是否存在點![]() ,使平行四邊形
,使平行四邊形![]() 為正方形?若存在,求出點
為正方形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ,②當點E為(4,-4)時,平行四邊形OEAF不是菱形;當點E為(3,-4)時,平行四邊形OEAF是菱形.③不存在這樣的點
,②當點E為(4,-4)時,平行四邊形OEAF不是菱形;當點E為(3,-4)時,平行四邊形OEAF是菱形.③不存在這樣的點![]() ,使平行四邊形
,使平行四邊形![]() 是正方形,理由見解析.
是正方形,理由見解析.
【解析】
(1)將拋物線解析式設成頂點式,然后用待定系數法就可解決問題.
(2)①求出拋物線與x軸的交點坐標,就可得到x的取值范圍,由于△OAE與△AOF全等,因此S=2S△OAE=-6y,然后把y換成x的代數式即可.
②易求出點E的縱坐標y,從而求出點E的坐標,然后算出OE、AE的長,就可判定四邊形OEAF是否為菱形;
③可先求出使四邊形OEAF是菱形時點E的坐標,然后再驗證菱形OEAF是否是正方形.
解:(1)由拋物線的對稱軸是![]() ,可設解析式為
,可設解析式為![]() .
.
把![]() 、
、![]() 兩點坐標代入上式,得
兩點坐標代入上式,得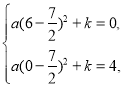
解得:![]() ,
,![]() .
.
∴拋物線的解析式為:![]() .
.
(2)①∵點![]() 在拋物線上,位于第四象限,
在拋物線上,位于第四象限,
∴![]() ,即
,即![]() ,
,![]() 表示點
表示點![]() 到
到![]() 的距離.
的距離.
∵![]() 是
是![]() 的對角線,
的對角線,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
∵拋物線與![]() 軸的兩個交點是
軸的兩個交點是![]() 和
和![]() ,
,
∴自變量![]() 的取值范圍是
的取值范圍是![]() ;
;
∴![]() ,(
,(![]() ).
).
②依題意,當![]() 時,即
時,即![]() ,
,
解得![]() ,
,![]() ;
;
Ⅰ.當x=4時,![]() ,則點E(4,-4).
,則點E(4,-4).
過點E作EH⊥x軸,垂足為H,如圖2,
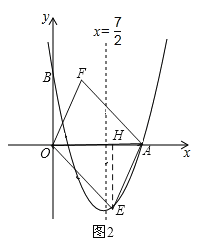
則有OH=4,EH=4,AH=2.
∵EH⊥x軸,
∴OE=![]() ,AE=
,AE=![]() .
.
∴OE≠AE.
∴平行四邊形OEAF不是菱形.
Ⅱ.當x=3時,![]() ,則點E(3,-4).
,則點E(3,-4).
過點E作EH⊥x軸,垂足為H,如圖3,
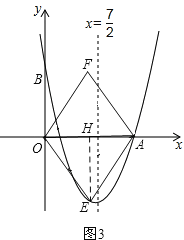
則有OH=3,EH=4,AH=3.
∵EH⊥x軸,
∴OE=5,AE=5.
∴OE=AE.
∴平行四邊形OEAF是菱形.
綜上所述;當點E為(4,-4)時,平行四邊形OEAF不是菱形;當點E為(3,-4)時,平行四邊形OEAF是菱形.
③不存在點E,使四邊形OEAF為正方形.
理由如下:
當點E在線段OA的垂直平分線上時,EO=EA,則平行四邊形OEAF是菱形,如圖4,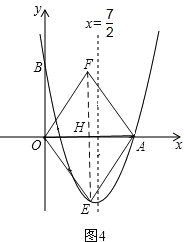
此時,![]() ,
,![]() ,,點E為(3,-4).
,,點E為(3,-4).
則有OA=6,EF=8.
∵OA≠EF,
∴菱形OEAF不是正方形.
∴不存在點E,使四邊形OEAF為正方形.


科目:初中數學 來源: 題型:
【題目】如圖,轉盤A中的6個扇形的面積相等,轉盤B中的3個扇形的面積相等.分別任意轉動轉盤A、B各1次,當轉盤停止轉動時,將指針所落扇形中的2個數字分別作為平面直角坐標系中一個點的橫坐標、縱坐標.
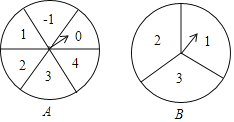
(1)用表格列出這樣的點所有可能的坐標;
(2)求這些點落在二次函數y=x2﹣5x+6的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】向陽中學為了解全校學生利用課外時間閱讀的情況,調查者隨機抽取若干名學生,調查他們一周的課外閱讀時間,并根據調查結果繪制了如下尚不完整的統計表(圖).根據圖表信息,解答下列問題:
頻率分布表
閱讀時間(小時) | 頻數(人) | 頻率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合計 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)將頻數分布直方圖補充完整;
(3)閱讀時間不低于5小時的6人中,有2名男生、4名女生.現從這6名學生中選取兩名同學進行讀書宣講,求選取的兩名學生恰好是兩名女生的概率.
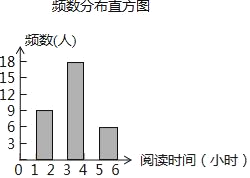
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年3月,我市某中學舉行了“愛我中國朗誦比賽”活動,根據學生的成績劃分為A、B、C、D四個等級,并繪制了不完整的兩種統計圖.根據圖中提供的信息,回答下列問題:
(1)參加朗誦比賽的學生共有 人,并把條形統計圖補充完整;
(2)扇形統計圖中,m= ,n= ;C等級對應扇形有圓心角為 度;
(3)學校欲從獲A等級的學生中隨機選取2人,參加市舉辦的朗誦比賽,請利用列表法或樹形圖法,求獲A等級的小明參加市朗誦比賽的概率.
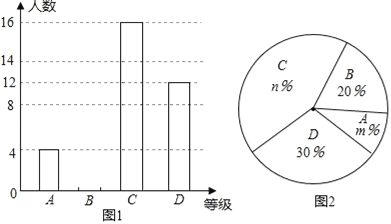
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“精準扶貧”這是新時期黨和國家扶貧工作的精髓和亮點.某校團委隨機抽取部分學生,對他們是否了解關于“精準扶貧”的情況進行調查,調查結果有三種:A、了解很多;B、了解一點;C、不了解.團委根據調查的數據進行整理,繪制了尚不完整的統計圖如下,圖1中C區域的圓心角為36°,請根據統計圖中的相關的信息,解答下列問題:
(1)求本次活動共調查了 名學生;圖1中,B區域的圓心角度是 ;在抽取的學生中調查結果的中位數落在 區域里.
(2)補全條形統計圖.
(3)若該校有1200名學生,請估算該校不是了解很多的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
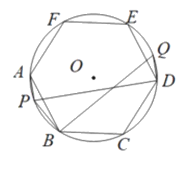
【題目】如圖,正六邊形ABCDEF內接于⊙O,在弧AB上取點P,連接AP,BP,過點D作DQ∥AP交⊙O于點Q,連接BQ. 已知BP=1,BQ=3,PQ的長為 ,AP的長為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
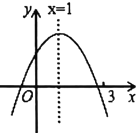
【題目】二次函數![]() 的圖象如圖所示,有下列結論:①
的圖象如圖所示,有下列結論:①![]() ;②
;②![]() ;③若
;③若![]() 為任意實數,則
為任意實數,則![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() ,且
,且![]() ,則
,則![]() .其中,正確結論的個數為( )
.其中,正確結論的個數為( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com