
【題目】以x為自變量的二次函數y=x2﹣2(b﹣2)x+b2﹣1的圖象不經過第三象限,則實數b的取值范圍是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
【答案】A
【解析】解:∵二次函數y=x2﹣2(b﹣2)x+b2﹣1的圖象不經過第三象限,
∵二次項系數a=1,
∴拋物線開口方向向上,
當拋物線的頂點在x軸上方時,
則b2﹣1≥0,△=[2(b﹣2)]2﹣4(b2﹣1)≤0,
解得b≥ ![]() ;
;
當拋物線的頂點在x軸的下方時,
設拋物線與x軸的交點的橫坐標分別為x1,x2,
∴x1+x2=2(b﹣2)>0,b2﹣1>0,
∴△=[2(b﹣2)]2﹣4(b2﹣1)>0,①
b﹣2>0,②
b2﹣1>0,③
由①得b< ![]() ,由②得b>2,
,由②得b>2,
∴此種情況不存在,
∴b≥ ![]() ,
,
所以答案是:A.
【考點精析】通過靈活運用二次函數圖象以及系數a、b、c的關系,掌握二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c)即可以解答此題.


科目:初中數學 來源: 題型:
【題目】已知:如圖,∠ABD和∠BDC的平分線交于點E,BE交CD于點F,∠1+∠2=90°.
(1)試說明:AB∥CD;
(2)試探究∠2與∠3的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,點
,點![]() 分別在
分別在![]() 直線上,點
直線上,點![]() 為兩平行線內部一點
為兩平行線內部一點

(1)如圖1,![]() 角平分線交于點N,若
角平分線交于點N,若![]() 等于
等于![]() ,求
,求![]() 的度數
的度數
(2)如圖2,點G為直線![]() 上一點,且
上一點,且![]() ,延長GM交直線AB于點Q,點P為MG上一點,射線
,延長GM交直線AB于點Q,點P為MG上一點,射線![]() 相交于點H,滿足
相交于點H,滿足![]() ,設
,設![]() ,求
,求![]() 的度數(用
的度數(用![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A,B的坐標分別為(1,0)、(4,0).將△ABC沿x軸向右平移,當點C落在直線y=2x﹣6上時,線段BC掃過的面積為( )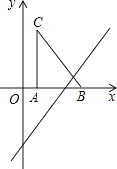
A.4
B.8
C.16
D.8 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c的圖象如圖所示,則下列四個結論:①a+b+c<0;②a+c=b;③b=﹣2a;④4ac﹣b2<0,其中正確的結論有( ) 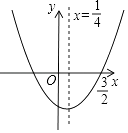
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 甲、乙兩名學生在參加今年體育考試前各做了5次立定跳遠測試,兩人的平均成績相同,其中甲所測得成績的方差是0.005,乙所測得的成績如下:2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,那么甲、乙的成績比較( )
A.甲的成績更穩定B.乙的成績更穩定
C.甲、乙的成績一樣穩定D.不能確定誰的成績更穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分18分)某校八(1)班同學為了解2011年某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行如下整理,
月均用水量 | 頻數(戶) | 頻率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |
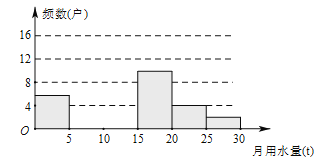
請解答以下問題:
(1)把上面的頻數分布表和頻數分布直方圖補充完整;
(2)若該小區用水量不超過15t的家庭占被調查家庭總數的百分比;
(3)若該小區有1000戶家庭,根據調查數據估計,該小區月均用水量超過20 t的家庭大約有多少戶?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com