
【題目】某水果商店以12.5元/千克的價格購進一批水果進行銷售,運輸過程中質量損耗5%,運輸費用是0.8元/千克(運輸費用按照進貨質量計算),假設不計其他費用.
(1)商店要把水果售完至少定價為多少元才不會虧本?
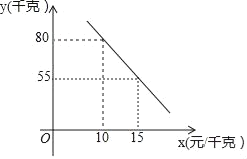
(2)在銷售過程中,商店發現每天水果的銷售量y(千克)與銷售單價x(元/千克)之間的函數關系如圖所示,那么當銷售單價定為多少時,每天獲得的利潤w最大?最大利潤是多少?
(3)該商店決定每銷售1千克水果就捐贈p元利潤(p≥1)給希望工程,通過銷售記錄發現,銷售價格大于每千克22元時,扣除捐贈后每天的利潤隨x增大而減小,直接寫出p的取值范圍.
【答案】(1)水果商要把水果售價至少定為14元/千克才不會虧本(2)當銷售單價定為20元時,每天獲得的利潤w最大,最大利潤是180元(3)1≤p≤4
【解析】
(1)設購進水果a千克,水果售價定為m元/千克,水果商才不會虧本,根據題意列出不等式即可求解;
(2)由(1)得y與銷售單價x之間的函數關系為:y=﹣5x+130,利用w=(x﹣14)y得到二次函數即可進行求解;
(3)設扣除捐贈后利潤為s,得s=(x﹣14﹣p)(﹣5x+130),根據對稱軸與函數的性質即可求解.
(1)設購進水果a千克,水果售價定為m元/千克,水果商才不會虧本,則有
am(1﹣5%)≥(12.5+0.8)a
則a>0可解得:m≥14
∴水果商要把水果售價至少定為14元/千克才不會虧本
(2)由(1)可知,每千克水果的平均成本為14元
得y與銷售單價x之間的函數關系為:y=﹣5x+130
由題意得:w=(x﹣14)y=(x﹣14)(﹣5x+130)=﹣5x2+200x﹣1820
整理得w=﹣5(x﹣20)2+180
∴當x=20時,w有最大值
∴當銷售單價定為20元時,每天獲得的利潤w最大,最大利潤是180元.
(3)設扣除捐贈后利潤為s
則s=(x﹣14﹣p)(﹣5x+130)=﹣5x2+(5p+200)x﹣130(p+14)
∵拋物線的開口向下
∴對稱軸為直線x=![]() =
=![]()
∵銷售價格大于每千克22元時,扣除捐贈后每天的利潤s隨x的增大而減小
∴![]() ≤22
≤22
解得p≤4
故1≤p≤4


科目:初中數學 來源: 題型:
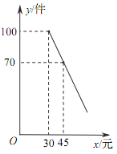
【題目】某商店購進一批成本為每件 30 元的商品,經調查發現,該商品每天的銷售量 y(件)與銷售單價 x(元)之間滿足一次函數關系,其圖象如圖所示.
(1)求該商品每天的銷售量 y 與銷售單價 x 之間的函數關系式;
(2)若商店按單價不低于成本價,且不高于 50 元銷售,則銷售單價定為多少,才能使銷售該商品每天獲得的利潤 w(元)最大?最大利潤是多少?
(3)若商店要使銷售該商品每天獲得的利潤不低于 800 元,則每天的銷售量最少應為多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】□ABCD中,E、F是對角線BD上不同的兩點,下列條件中,不能得出四邊形AECF一定為平行四邊形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中數學 來源: 題型:
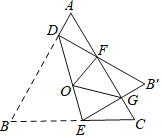
【題目】如圖,等邊三角形ABC邊長是定值,點O是它的外心,過點O任意作一條直線分別交AB,BC于點D,E.將△BDE沿直線DE折疊,得到△B′DE,若B′D,B′E分別交AC于點F,G,連接OF,OG,則下列判斷錯誤的是( )
A. △ADF≌△CGE
B. △B′FG的周長是一個定值
C. 四邊形FOEC的面積是一個定值
D. 四邊形OGB'F的面積是一個定值
查看答案和解析>>
科目:初中數學 來源: 題型:
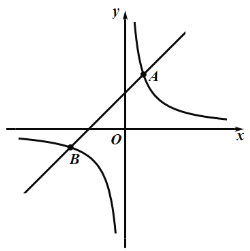
【題目】如圖:反比例函數 與一次函數 的圖象交于A(1,3)和B(-3,n)兩點.
(1)求反比例函數與一次函數的解析式;
(2)當x取什么值時,一次函數的值大于反比例函數的值.
(3)求出△OAB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
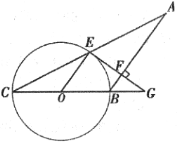
【題目】如圖,在△ABC中,AB=BC,以BC為直徑作⊙ O交AC于點E,過點E作AB的垂線交AB于點F,交CB的延長線于點G.
(1)求證:EG是⊙O的切線;
(2)若BG=OB,AC=6,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于A(m,6),B(3,n)兩點.
的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)求![]() 的面積;
的面積;
(3)根據圖象直接寫出![]() 的x的取值范圍
的x的取值范圍

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com