
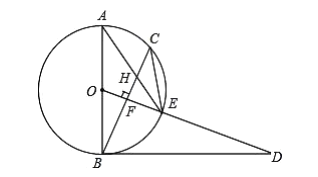
【題目】已知,如圖,![]() 是⊙
是⊙![]() 的直徑,點
的直徑,點![]() 為⊙
為⊙![]() 上一點,
上一點,![]() 于點
于點![]() ,交⊙
,交⊙![]() 于點
于點![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 為
為![]() 的延長線上一點,且
的延長線上一點,且![]() .
.
(1)試判斷直線![]() 與⊙
與⊙![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)若⊙![]() 的半徑為
的半徑為![]() ,
,![]() ,求
,求![]() 的長.
的長.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,![]() 是矩形
是矩形![]() 內的任意一點,連接
內的任意一點,連接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,設它們的面積分別是
,設它們的面積分別是![]() ,
,![]() ,
,![]() ,
,![]() , 給出如下結論:①
, 給出如下結論:①![]() ②
②![]() ③若
③若![]() ,則
,則![]() ④若
④若![]() ,則
,則![]() 點在矩形的對角線上.其中正確的結論的序號是( )
點在矩形的對角線上.其中正確的結論的序號是( )

A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】類比梯形的定義,我們定義:有一組對角相等而另一組對角不相等的凸四邊形叫做“等對角四邊形”.
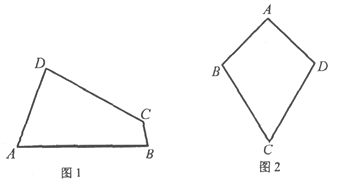
(1)已知:如圖1,四邊形ABCD是“等對角四邊形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度數.
(2)在探究“等對角四邊形”性質時:
①小紅畫了一個“等對角四邊形”ABCD(如圖2),其中∠ABC=∠ADC,AB=AD,此時她發現CB=CD成立.請你證明此結論;
②由此小紅猜想:“對于任意‘等對角四邊形’,當一組鄰邊相等時,另一組鄰邊也相等”.你認為她的猜想正確嗎?若正確,請證明;若不正確,請舉出反例.
(3)已知:在“等對角四邊形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求對角線AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的
的![]() 與
與![]() 的部分對應值如表:
的部分對應值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列結論:![]() 拋物線的開口向上;②拋物線的對稱軸為直線
拋物線的開口向上;②拋物線的對稱軸為直線![]() ;③當
;③當![]() 時,
時,![]() ;④拋物線與
;④拋物線與![]() 軸的兩個交點間的距離是
軸的兩個交點間的距離是![]() ;⑤若
;⑤若![]() 是拋物線上兩點,則
是拋物線上兩點,則![]() ,其中正確的個數是( )
,其中正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
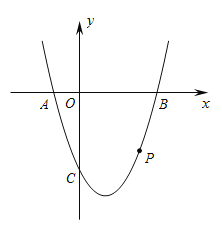
【題目】如圖,拋物線![]() 與x軸相交于
與x軸相交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸相交于點
軸相交于點![]() .
.![]() 為拋物線上一點,橫坐標為
為拋物線上一點,橫坐標為![]() ,且
,且![]() .
.
⑴求此拋物線的解析式;
⑵當點![]() 位于
位于![]() 軸下方時,求
軸下方時,求![]() 面積的最大值;
面積的最大值;
⑶設此拋物線在點![]() 與點
與點![]() 之間部分(含點
之間部分(含點![]() 和點
和點![]() )最高點與最低點的縱坐標之差為
)最高點與最低點的縱坐標之差為![]() .
.
①求![]() 關于
關于![]() 的函數解析式,并寫出自變量
的函數解析式,并寫出自變量![]() 的取值范圍;
的取值范圍;
②當![]() 時,直接寫出
時,直接寫出![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(教材呈現)
下圖是華師版九年級上冊數學教材第79頁的部分內容.

請根據教材內容,結合圖①,寫出完整的解題過程.
(結論應用)
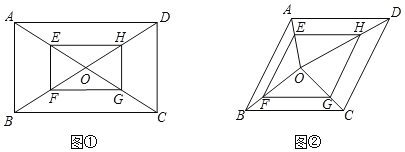
(1)在圖①中,若AB=2,∠AOD=120°,則四邊形EFGH的面積為______.
(2)如圖②,在菱形ABCD中,∠BAD=120°,O是其內任意一點,連接O與菱形ABCD各頂點,四邊形EFGH的頂點E、F、G、H分別在AO、BO、CO、DO上,EO=2AE,EF∥AB∥GH,且EF=GH,若△EFO與△GHO的面積和為![]() ,則菱形ABCD的周長為______.
,則菱形ABCD的周長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點C沿著某條路徑運動,以點C為旋轉中心,將點A(0,4)逆時針旋轉90°到點B(m,1),若﹣5≤m≤5,則點C運動的路徑長為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某批發商以每件50元的價格購進800件T恤,第一個月以單價80元銷售,售出了200件;第二個月如果單價不變,預計仍可售出200件,批發商為增加銷售量,決定降價銷售,根據市場調查,單價每降低1元,可多售出10件,但最低單價應高于購進的價格;第二個月結束后,批發商將對剩余的T恤一次性清倉銷售,清倉是單價為40元.如果批發商希望通過銷售這批T恤獲利9000元,那么第二個月的單價應是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
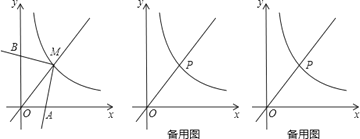
【題目】如圖,反比例函數y=![]() (x>0)的圖象與直線y=x交于點M,∠AMB=90°,其兩邊分別與兩坐標軸的正半軸交于點A,B,四邊形OAMB的面積為6.
(x>0)的圖象與直線y=x交于點M,∠AMB=90°,其兩邊分別與兩坐標軸的正半軸交于點A,B,四邊形OAMB的面積為6.
(1)求k的值;
(2)點P在反比例函數y=![]() (x>0)的圖象上,若點P的橫坐標為3,∠EPF=90°,其兩邊分別與x軸的正半軸,直線y=x交于點E,F,問是否存在點E,使得PE=PF?若存在,求出點E的坐標;若不存在,請說明理由.
(x>0)的圖象上,若點P的橫坐標為3,∠EPF=90°,其兩邊分別與x軸的正半軸,直線y=x交于點E,F,問是否存在點E,使得PE=PF?若存在,求出點E的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com