
如圖,在平面直角坐標系中,正方形ABCD的頂點O在坐標原點,點B的坐標為(1,4),點A在第二象限,反比例函數y=
 的圖象經過點A,則k的值是( )
的圖象經過點A,則k的值是( )


A.﹣2 B.﹣4 C.﹣
 D.
D.

C【考點】反比例函數圖象上點的坐標特征.
【分析】作AD⊥x軸于D,CE⊥x軸于E,先通過證得△AOD≌△OCE得出AD=OE,OD=CE,設A(x,
 ),則C(
),則C(
 ,﹣x),根據正方形的性質求得對角線解得F的坐標,根據直線OB的解析式設出直線AC的解析式為:y=﹣
,﹣x),根據正方形的性質求得對角線解得F的坐標,根據直線OB的解析式設出直線AC的解析式為:y=﹣
 x+b,代入交點坐標求得解析式,然后把A,C的坐標代入即可求得k的值.
x+b,代入交點坐標求得解析式,然后把A,C的坐標代入即可求得k的值.
【解答】解:作AD⊥x軸于D,CE⊥x軸于E,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,

 ,
,
∴△AOD≌△OCE(AAS),
∴AD=OE,OD=CE,
設A(x,
 ),則C(
),則C(
 ,﹣x),
,﹣x),
∵點B的坐標為(1,4),
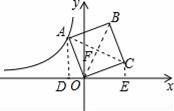
∴OB=
 =
=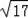
 ,
,
直線OB為:y=4x,
∵AC和OB互相垂直平分,
∴它們的交點F的坐標為(
 ,2),
,2),
設直線AC的解析式為:y=﹣
 x+b,
x+b,
代入(
 ,2)得,2=﹣
,2)得,2=﹣
 ×
×
 +b,解得b=
+b,解得b=
 ,
,
直線AC的解析式為:y=﹣
 x+
x+
 ,
,
把A(x,
 ),C(
),C(
 ,﹣x)代入得
,﹣x)代入得

 ,解得k=﹣
,解得k=﹣
 .
.
故選C.

【點評】本題考查了反比例函數圖象上點的坐標特征,待定系數法求解析式,正方形的性質,三角形求得的判定和性質,熟練掌握正方形的性質是解題的關鍵.


科目:初中數學 來源: 題型:
閱讀下列材料:
(1)關于x的方程x2﹣3x+1=0(x≠0)方程兩邊同時乘以
 得:
得:
 即
即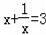
 ,
,



(2)a3+b3=(a+b)(a2﹣ab+b2);a3﹣b3=(a﹣b)(a2+ab+b2).
根據以上材料,解答下列問題:
(1)x2﹣4x+1=0(x≠0),則
 = 4 ,
= 4 ,
 = 14 ,
= 14 ,
 = 194 ;
= 194 ;
(2)2x2﹣7x+2=0(x≠0),求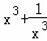
 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于點D,動點P從點A出發以每秒1厘米的速度在線段AD上向終點D運動.設動點運動時間為t秒.

(1)求AD的長;
(2)當△PDC的面積為15平方厘米時, 求t的值;
求t的值;
(3)動點M從點C出發以每秒2厘米的速度在射線CB上運動.點M與點P同時出發,且當點P運動到終點D時,點M也停止運動.是否存在t,使得S△PMD= S△ABC?若存在,請求出t的值;若不存在,請說明理由.
S△ABC?若存在,請求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
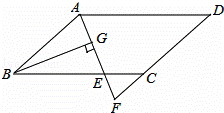
如圖,在平行四邊形ABCD中,AB=6,AD=9,∠BAD的平分線交BC于
點E,交DC的延長線于點F,BG⊥AE于G,BG=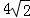 ,則梯形AECD的
,則梯形AECD的
周長( )
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中數學 來源: 題型:
大雙,小雙的媽媽申購到一張北京奧運會的門票,兄弟倆決定分別用標有數字且除數字以外沒有其它任何區別的小球,各自設計一種游戲確定誰去.
大雙:A袋中放著分別標有數字1,2,3的三個小球,B袋中放著分別標有數字4,5的兩個小球,且都已各自攪勻,小雙蒙上眼睛從兩個口袋中各取出1個小球,若兩個小球上的數字之積為偶數,則大雙得到門票;若積為奇數,則小雙得到門票.
小雙:口袋中放著分別標有數字1,2,3的三個小球,且已攪勻,大雙,小雙各蒙上眼睛有放回地摸1次,大雙摸到偶數就記2分,摸到奇數記0分;小雙摸到奇數就記1分,摸到偶數記0分,積分多的就得到門票.(若積分相同,則重復第二次.)
(1)大雙設計的游戲方案對雙方是否公平?請你運用列表或樹狀圖說明理由;
(2)小雙設計的游戲方案對雙方是否公平?不必說理.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com