
分析 ①根據方程的系數結合根的判別式即可得出△=(a-b)2+4>0,由此即可得出x1≠x2,結論①成立;②由根與系數的關系即可得出x1x2=ab-1,由此即可得出x1x2<ab,結論②成立;③由根與系數的關系可得出x1+x2=a+b、x1x2=ab-1,將x12+x22變形為$({x}_{1}+{x}_{2})^{2}$-2x1x2,代入數據即可得出x12+x22=a2+b2+2,進而可得出x12+x22>a2+b2,結論③成立;④結合③中的x12+x22=a2+b2+2以及x1+x2=a+b、x1x2=ab-1即可得出${(x}_{1}-{x}_{2})^{2}$=(a-b)2+4,由此即可得出${(x}_{1}-{x}_{2})^{2}$>(a-b)2,再根據a>b、x1>x2,即可得出x1-x2>a-b,結論④不成立.綜上即可得出結論.
解答 解:①∵在方程x2-(a+b)x+ab-1=0中,△=[-(a+b)]2-4(ab-1)=a2+b2+2ab-4ab+4=(a-b)2+4>0,
∴x1≠x2,結論①成立;
②∵x1、x2是方程x2-(a+b)x+ab-1=0的兩個實數根,
∴x1x2=ab-1<ab,結論②成立;
③∵x1、x2是方程x2-(a+b)x+ab-1=0的兩個實數根,
∴x1+x2=a+b,x1x2=ab-1,
∴x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1x2=(a+b)2-2(ab-1)=a2+b2+2ab-2ab+2=a2+b2+2>a2+b2,結論③成立;
④∵x1+x2=a+b,x1x2=ab-1,
∴${(x}_{1}-{x}_{2})^{2}$=x12+x22-2x1x2=a2+b2+2-2(ab-1)=(a-b)2+4,
∴${(x}_{1}-{x}_{2})^{2}$>(a-b)2.
又∵a>b,x1>x2,
∴x1-x2>a-b,結論④不成立.
故答案為:①②③.
點評 本題考查了根與系數的關系、根的判別式以及完全平方公式,逐一分析四條結論是否成立是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在平面直角坐標系中,把直線y=3x沿y軸向下平移后得到直線AB,如果點N(m,n)是直線AB上的一點,且3m-n=2,那么直線AB的函數表達式為y=3x-2.
如圖,在平面直角坐標系中,把直線y=3x沿y軸向下平移后得到直線AB,如果點N(m,n)是直線AB上的一點,且3m-n=2,那么直線AB的函數表達式為y=3x-2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
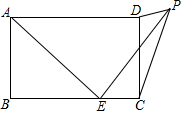 如圖,在矩形ABCD中,AB=3,BC=5,點E為BC邊上一個動點,連接AE,將線段AE繞點E順時針旋轉90°,點A落在點P處,當點P在矩形ABCD外部時,連接PC、PD.若△DPC為直角三角形,則BE的長為3或$\frac{5+\sqrt{17}}{2}$.
如圖,在矩形ABCD中,AB=3,BC=5,點E為BC邊上一個動點,連接AE,將線段AE繞點E順時針旋轉90°,點A落在點P處,當點P在矩形ABCD外部時,連接PC、PD.若△DPC為直角三角形,則BE的長為3或$\frac{5+\sqrt{17}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 加數的個數n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com