
【題目】如圖,點 O 是等邊△ABC 內一點,∠AOB=110°,∠BOC=a.將△BOC 繞點 C 按順時針方向旋轉 60°得△ADC,則△ADC≌△BOC,連接 OD.
(1)求證:△COD 是等邊三角形;
(2)當α=120°時,試判斷 AD 與 OC 的位置關系,并說明理由;
(3)探究:當 a 為多少度時,△AOD 是等腰三角形?

【答案】(1)證明見解析;(2)證明見解析;(3)當 a 為 125°或 110°或 140°時,△AOD 是等腰三角形.
【解析】
(1)根據旋轉得出CO=CD,∠DCO=60°,根據等邊三角形的判定推出即可.
(2)求出∠ADO=∠COD=60°,根據平行線的判定推出即可.
(3)用∠α表示∠ADO、∠AOD、∠DAO,分為三種情況:①∠ADO=∠AOD,②∠ADO=∠OAD,③∠OAD=∠AOD,代入求出即可.
證明:(1)∵△ADC≌△BOC,
∴CO=CD,
∵將△BOC 繞點 C 按順時針方向旋轉 60°得△ADC,
∴∠DCO=60°,
∴△COD 是等邊三角形.
(2)解:AD∥OC,
理由是:∵△DOC 是等邊三角形,
∴∠CDO=∠DOC=60°,
∵∠α=120°,△COB≌△CDA,
∴∠ADC=∠COB=120°,
∴∠ADO=120°﹣60°=60°,
∴∠ADO=∠DOC=60°,
∴AD∥OC.
(3)解:∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣110°﹣∠α﹣60°=190°﹣∠α,∠ADO=∠ADC﹣∠CDO=∠α﹣60°,∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(190°﹣∠α)=50°, 若∠ADO=∠AOD,即∠α﹣60°=190°﹣∠α,
解得:∠α=125°;
若∠ADO=∠OAD,則∠α﹣60°=50°, 解得:∠α=110°;
若∠OAD=∠AOD,即 50°=190°﹣∠α, 解得:∠α=140°;
即當 a 為 125°或 110°或 140°時,△AOD 是等腰三角形.


科目:初中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,點
中,點![]() 、
、![]() 分別在函數
分別在函數![]() 與
與![]() 的圖象上,
的圖象上, ![]() 、
、![]() 的橫坐標分別為
的橫坐標分別為![]() 、
、![]() 。
。

(1)若![]() 軸,求
軸,求![]() 的面積;
的面積;
(2)若![]() 是以
是以![]() 為底邊的等腰三角形,且a
為底邊的等腰三角形,且a![]() ,求
,求![]() 的值;
的值;
(3)作邊長為2的正方形![]() ,使
,使![]() 軸,點
軸,點![]() 在點
在點![]() 的左上方,那么,對大于或等于的任意實數
的左上方,那么,對大于或等于的任意實數![]() ,
, ![]() 邊與函數
邊與函數![]() 的圖象都有交點,請說明理由。
的圖象都有交點,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一個直徑為1m的圓形鐵皮,要從中剪出一個最大的圓心角為90°的扇形ABC,如圖所示.
(1)求被剪掉陰影部分的面積:
(2)用所留的扇形鐵皮圍成一個圓錐,該圓錐的底面圓的半徑是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣2(k﹣1)x+k2=0,
(1)當k為何值時,方程有實數根;
(2)設x1,x2是方程的兩個實數根,且x12+x22=4,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知x2+(a+3)x+a+1=0是關于x的一元二次方程.
(1)求證:方程總有兩個不相等的實數根;
(2)若方程的兩個實數根為x1 ,x2 ,且x12+x22=10,求實數a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在電線桿上的C處引拉線CE、CF固定電線桿,拉線CE和地面成60°角,在離電線桿6米的B處安置測角儀,在A處測得電線桿上C處的仰角為30°,已知測角儀高AB為1.5米,求拉線CE的長(結果保留根號).

查看答案和解析>>
科目:初中數學 來源: 題型:
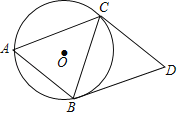
【題目】如圖,已知⊙O是△ABC的外接圓,且AB=BC=CD,AB∥CD,連接BD.
(1)求證:BD是⊙O的切線;
(2)若AB=10,cos∠BAC=![]() ,求BD的長及⊙O的半徑.
,求BD的長及⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店銷售A、B兩種文具,其中A文具的定價為20元/件,B產品的定價10元/件.
(1)若該文具按定價售出A、B兩種文具共400件,若銷售總額不低于5000元,則至少銷售A產品多少件?
(2)該文具店2018年2月按定價銷售A文具280件,B文具120件,2018年3月,市場情況發生變化,A文具銷售價與上個月持平,但這個月的銷售量比上個月減少了m%;B文具的銷售價比上個月減少了m%,但銷售量增加了![]() m%;3月份的銷售總金額與2月份保持不變.求m的值.
m%;3月份的銷售總金額與2月份保持不變.求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,某學校開展“交通安全日”活動.在活動中,交警叔叔向同學們展示了大貨車盲區的分布情況,并提醒大家:坐在駕駛室的司機根本看不到在盲區中的同學們,所以一定要遠離大貨車的盲區,保護自身安全.小剛所在的學習小組為了更好的分析大貨車盲區的問題,將圖1用平面圖形進行表示,并標注了測量出的數據,如圖2.在圖2中大貨車的形狀為矩形,而盲區1為梯形,盲區2、盲區3為直角三角形,盲區4為正方形.
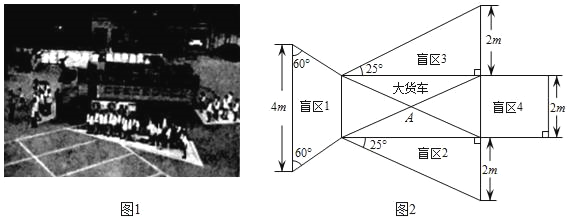
請你幫助小剛的學習小組解決下面的問題:
(1)盲區1的面積約是多少m2;盲區2的面積約是多少m2;
(![]() ≈1.4,
≈1.4,![]() ≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,結果保留整數)
≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,結果保留整數)
(2)如果以大貨車的中心A點為圓心,覆蓋所有盲區的半徑最小的圓為大貨車的危險區域,請在圖2中畫出大貨車的危險區域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com