【題目】如圖（1），在
ABC中，
，BC=9cm, AC=12cm, AB=15cm.現(xiàn)有一動點P，從點A出發(fā)，沿著三角形的邊AC
CBBA運動，回到點A停止，速度為3cm/s，設(shè)運動時間為t s．
（1）如圖（1），當(dāng)t=______時，△APC的面積等于△ABC面積的一半；
（2）如圖（2），在△DEF中，
，DE=4cm, DF=5cm, 
． 在△ABC的邊上，若另外有一個動點Q，與點P同時從點A出發(fā)，沿著ABBCCA運動，回到點A停止．在兩點運動過程中的某一時刻，恰好
，求點Q的運動速度．
【答案】（1）t=
或
；（2）
【解析】
（1）先求出△ABC面積，進而可求出△APC的面積，分P點運動到BC邊上時和P點運動到AB邊上時兩種情況分別討論即可；
（2）由全等三角形的性質(zhì)得出
，進而可求出P的運動時間，即Q的運動時間，再利用速度=路程÷時間求解即可．
（1）
∵△APC的面積等于△ABC面積的一半
當(dāng)P點運動到BC邊上時，此時
即
此時
當(dāng)P點運動到AB邊上時，作PQ⊥AC于Q
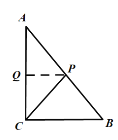
此時
即
∴此時P點在AB邊的中點
此時
綜上所述，當(dāng)t=或時，△APC的面積等于△ABC面積的一半
（2）∵
，DE=4cm, DF=5cm,
此時P點運動的時間為
∵P,Q同時出發(fā)，所以Q運動的時間也是
∴Q運動的速度為
科目：初中數(shù)學(xué) 來源： 題型：
【題目】數(shù)學(xué)課上，李老師出示了如下框中的題目．
在等邊三角形ABC中，點E在AB上，點D在CB的延長線上，且ED=EC，如圖．試確定線段AE與DB的大小關(guān)系，并說明理由． |
|
小敏與同桌小聰討論后，進行了如下解答：
（1）特殊情況，探索結(jié)論
當(dāng)點E為AB的中點時，如圖1，確定線段AE與的DB大小關(guān)系．請你直接寫出結(jié)論：
AE DB(填“＞”，“＜”或“＝”)．
圖1 圖2
（2）特例啟發(fā)，解答題目
解：題目中，AE與DB的大小關(guān)系是：AE DB(填“＞”，“＜”或“＝”)．
理由如下：如圖2，過點E作EF∥BC，交AC于點F.
(請你完成以下解答過程)
（3）拓展結(jié)論，設(shè)計新題
在等邊三角形ABC中，點E在直線AB上，點D在直線BC上，且ED=EC．若△ABC的邊長為1，AE=2，求CD的長(請你直接寫出結(jié)果)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，
是等邊三角形，點
在
上，點
在
的延長線上,且
．
(1)如圖甲，若點是的中點，求證： 
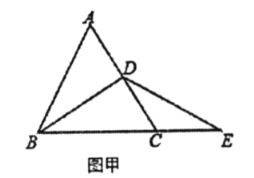
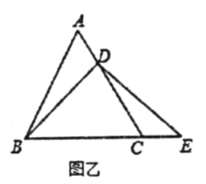
(2)如圖乙，若點不的中點，
是否成立?證明你的結(jié)論．
(3)如圖丙，若點在線段的延長線上，試判斷
與
的大小關(guān)系，并說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
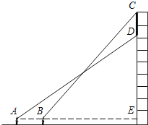
【題目】如圖所示，小楊在廣場上的
處正面觀測一座樓房墻上的廣告屏幕，測得屏幕下端
處的仰角為
，然后他正對大樓方向前進
到達
處，又測得該屏幕上端
處的仰角為
．若該樓高為
，小楊的眼睛離地面
，廣告屏幕的上端與樓房的頂端平齊．求廣告屏幕上端與下端之間的距離
是________
（取
，結(jié)果精確到
）．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，已知二次函數(shù)經(jīng)過點B（3，0），C（0，3），D（4，-5）
（1）求拋物線的解析式；
（2）求△ABC的面積；
（3）若P是拋物線上一點，且S△ABP=
S△ABC，這樣的點P有幾個請直接寫出它們的坐標(biāo)．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
