
【題目】如圖,在△ABC中,AB=AC=4,∠BAC=120°,AD為BC邊上的高,點(diǎn)P從點(diǎn)B以每秒![]() 個(gè)單位長度的速度向終點(diǎn)C運(yùn)動(dòng),同時(shí)點(diǎn)Q從點(diǎn)C以每秒1個(gè)單位長度的速度向終點(diǎn)A運(yùn)動(dòng),其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),兩點(diǎn)同時(shí)停止.
個(gè)單位長度的速度向終點(diǎn)C運(yùn)動(dòng),同時(shí)點(diǎn)Q從點(diǎn)C以每秒1個(gè)單位長度的速度向終點(diǎn)A運(yùn)動(dòng),其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),兩點(diǎn)同時(shí)停止.
(1)求BC的長;
(2)設(shè)△PDQ的面積為S,點(diǎn)P的運(yùn)動(dòng)時(shí)間為t秒,求S與t的函數(shù)關(guān)系式,并寫出自變量的取值范圍;
(3)在動(dòng)點(diǎn)P、Q的運(yùn)動(dòng)過程中,是否存在PD=PQ,若存在,求出△PDQ的周長,若不存在,請(qǐng)說明理由.

【答案】(1) 4![]() ;(2)①S△PDQ=-
;(2)①S△PDQ=-![]() t2+
t2+![]() t(0≤t≤2);②S△PDQ=
t(0≤t≤2);②S△PDQ=![]() t -
t -![]() t2 (2<t≤4);(3)存在PD=PQ,此時(shí)△PDQ的周長為3
t2 (2<t≤4);(3)存在PD=PQ,此時(shí)△PDQ的周長為3![]() .
.
【解析】
(1)根據(jù)等腰三角形性質(zhì)三線合一和含30°銳角的直角三角形的性質(zhì)即可解答;(2)分當(dāng)點(diǎn)P在線段BD上運(yùn)動(dòng)和當(dāng)點(diǎn)P在線段DC上運(yùn)動(dòng),過點(diǎn)Q作QM⊥BC于點(diǎn)M,用含時(shí)間t的代數(shù)式分別表示出PD=BD-BP=2![]() -
-![]() t或者PD= BP - BD =
t或者PD= BP - BD =![]() t- 2
t- 2![]() ,、QM
,、QM ![]() CQ=
CQ=![]() t的長,根據(jù)三角形面積公式即可求解;(3)根據(jù)題意可得,當(dāng)PD=PQ時(shí),PD=PQ,
t的長,根據(jù)三角形面積公式即可求解;(3)根據(jù)題意可得,當(dāng)PD=PQ時(shí),PD=PQ,
用含t的式子分別表示出Rt△PMQ的三邊,由勾股定理得QM2+MP2=QP2,解得t=3后得到△DPQ是等邊三角形,邊長為![]() ,從而求出周長.
,從而求出周長.
解:(1)△ABC中,∵AB=AC=4,∠BAC=120°,AD⊥ BC,
∴∠B=∠C=30°,BD=DC
∴AD=![]() AB=2,由勾股定理得:BD=DC= 2
AB=2,由勾股定理得:BD=DC= 2![]()
∴BC=2BD=4![]() ;
;
(2)過點(diǎn)Q作QM⊥BC于點(diǎn)M,
∵CQ=t,∠C=30°,BP=![]() t
t
∴QM= ![]() CQ=
CQ=![]() t ,
t ,
①當(dāng)點(diǎn)P在線段BD上運(yùn)動(dòng)時(shí),即0≤t≤2,如圖:
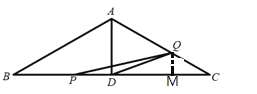
PD=BD-BP=2![]() -
-![]() t
t
∴S△PDQ=![]() ×PD×QM=
×PD×QM=![]() ×(2
×(2![]() -
-![]() t)×
t)×![]() t=-
t=-![]() t2+
t2+![]() t(0≤t≤2);
t(0≤t≤2);
②當(dāng)點(diǎn)P在線段DC上運(yùn)動(dòng)時(shí),即2<t≤4,如圖:
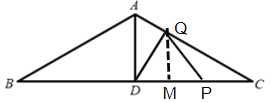
PD= BP - BD =![]() t- 2
t- 2![]() ,方法同①得:
,方法同①得:
S△PDQ=![]() ×PD×QM=
×PD×QM=![]() ×(
×(![]() t -2
t -2![]() )×
)×![]() t=
t=![]() t -
t -![]() t2 (2<t≤4);
t2 (2<t≤4);
(3)當(dāng)點(diǎn)P在BD上運(yùn)動(dòng)時(shí),∠BDQ>90°,PD≠PQ,所以若PD=PQ=![]() t -2
t -2![]() ,則PD=PQ如(2)②中圖形,此時(shí)PD=PQ=
,則PD=PQ如(2)②中圖形,此時(shí)PD=PQ=![]() t- 2
t- 2![]() ,PC=BC-BP=4
,PC=BC-BP=4![]() -
-![]() t,MC=
t,MC=![]() =
=![]() t ,MP=MC-PC=
t ,MP=MC-PC=![]() t-(4
t-(4![]() -
-![]() t)=
t)=![]() t-4
t-4![]() ,
,
Rt△PMQ中,∵QM2+MP2=QP2
∴(![]() t)2+(
t)2+(![]() t-4
t-4![]() )2=(
)2=(![]() t -2
t -2![]() )2,
)2,
化簡得:t2-6t+9=0,即(t-3)2=9,∵t >0
解得t=3,即PD=PQ=![]() t -2
t -2![]() =3
=3![]() -2
-2![]() =
=![]() =PC,
=PC,
又∵∠C=30°,∴∠C=∠PQC=30°,∠DPQ=∠C+∠PQC=60°,即△DPQ是等邊三角形,
∴△DPQ的周長=3PD=3![]() .
.


 考前必練系列答案
考前必練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
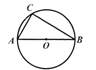
【題目】如圖,⊙O是△ABC的外接圓,AB是⊙O的直徑,AB=8.
(1)利用尺規(guī),作∠CAB的平分線,交⊙O于點(diǎn)D;(保留作圖痕跡,不寫作法)
(2)在(1)的條件下,連接CD,OD,若AC=CD,求∠B的度數(shù);
(3)在(2)的條件下,OD交BC于點(diǎn)E.求出由線段ED,BE,![]() 所圍成區(qū)域的面積.(其中
所圍成區(qū)域的面積.(其中![]() 表示劣弧,結(jié)果保留π和根號(hào))
表示劣弧,結(jié)果保留π和根號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題中:
①長為![]() 的線段
的線段![]() 沿某一方向平移
沿某一方向平移![]() 后,平移后線段
后,平移后線段![]() 的長為
的長為![]() ;
;
②三角形的高在三角形內(nèi)部;
③六邊形的內(nèi)角和是外角和的兩倍;
④平行于同一直線的兩直線平行;
⑤兩個(gè)角的兩邊分別平行,則這兩個(gè)角相等,真命題個(gè)數(shù)有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】計(jì)算:
(1)(﹣5)﹣(+3)+(﹣9)﹣(﹣7)
(2)(+5![]() )+(﹣3
)+(﹣3![]() )+(﹣6
)+(﹣6![]() )+(﹣15
)+(﹣15![]() )
)
(3)|﹣6![]() |+(﹣8)+|﹣3﹣
|+(﹣8)+|﹣3﹣![]() |
|
(4)78×(﹣![]() )+(﹣11)×(﹣
)+(﹣11)×(﹣![]() )+(﹣33)×0.6
)+(﹣33)×0.6
(5)(﹣2)2010×(﹣0.5)2009+(﹣6![]() )×7
)×7
(6)﹣14﹣![]() ×[2﹣(﹣3)﹣2]
×[2﹣(﹣3)﹣2]
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,動(dòng)點(diǎn)P從點(diǎn)B出發(fā),在BA邊上以每秒5cm的速度向點(diǎn)A勻速運(yùn)動(dòng),同時(shí)動(dòng)點(diǎn)Q從點(diǎn)C出發(fā),在CB邊上以每秒4cm的速度向點(diǎn)B勻速運(yùn)動(dòng),運(yùn)動(dòng)時(shí)間為t秒(0<t<2),連接PQ.
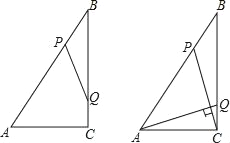
(1)若△BPQ與△ABC相似,求t的值;
(2)連接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場(chǎng)購進(jìn)一批單價(jià)為4元的日用品.若按每件5元的價(jià)格銷售,每月能賣出300件;若按每件6元的價(jià)格銷售,每月能賣出200件,假定每月銷售件數(shù)![]() (件)與價(jià)格
(件)與價(jià)格![]() (元/件)之間滿足一次函數(shù)關(guān)系.
(元/件)之間滿足一次函數(shù)關(guān)系.
(1)、試求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)、當(dāng)銷售價(jià)格定為多少時(shí),才能使每月的利潤最大?每月的最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=(m-2)x2+(m+3)x+m+2的圖象過點(diǎn)(0,5)
(1)求m的值,并寫出二次函數(shù)的表達(dá)式;
(2)求出二次函數(shù)圖象的頂點(diǎn)坐標(biāo)、對(duì)稱軸。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
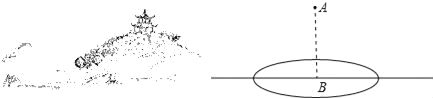
【題目】如圖,湖心島上有一涼亭,現(xiàn)欲利用湖岸邊的開闊平整地帶,測(cè)量涼亭頂端到湖面所在平面的高度AB(見示意圖),可供使用的工具有測(cè)傾器、皮尺.
(1)請(qǐng)你根據(jù)現(xiàn)有條件,設(shè)計(jì)一個(gè)測(cè)量涼亭頂端到湖面所在平面的高度AB的方案,畫出測(cè)量方案的平面示意圖,并將測(cè)量的數(shù)據(jù)標(biāo)注在圖形上(所測(cè)的距離用m,n,…表示,角用α,β,…表示,測(cè)傾器高度忽略不計(jì));
(2)根據(jù)你所測(cè)量的數(shù)據(jù),計(jì)算涼亭到湖面的高度AB(用字母表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
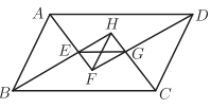
【題目】如圖,平行四邊形ABCD的四個(gè)內(nèi)角的平分線相交成四邊形EFGH,求證:
(1)EG=HF.
(2)EG=BC-AB.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com