
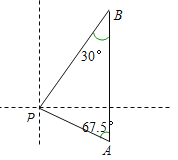
【題目】馬航MH370 客機(jī)“失聯(lián)”,我國“海巡01號”前往搜尋。如圖某天上午9時,“海巡01號” 輪船位于A處,觀測到某小島P位于輪船的北偏西67.5°,輪船以21海里/時的速度向正北方向行駛,下午2時該船到達(dá)B處,這時觀測到小島P位于該船的南偏西30°方向,求此時輪船所處位置B與小島P的距離?(精確到0.1)

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解答
(1)如圖,在直線m的同側(cè)有A,B兩點(diǎn),在直線m上找點(diǎn)P,Q,使PA+PB最小,|QB﹣QA|最大(保留作圖痕跡) 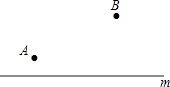
(2)平面直角坐標(biāo)系內(nèi)有兩點(diǎn)A(2,3),B(4,5),請分別在x軸,y軸上找點(diǎn)P,Q,使PA+PB最小,|QB﹣QA|最大,則點(diǎn)P,Q的坐標(biāo)分別為 ,
(3)代數(shù)式 ![]() +
+ ![]() 的最小值是 , 此時x=
的最小值是 , 此時x=
(4)代數(shù)式 ![]() ﹣
﹣ ![]() 的最大值是 , 此時x= .
的最大值是 , 此時x= .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
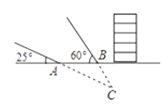
【題目】某探測隊在地面A、B兩處均探測出建筑物下方C處有生命跡象,已知探測線與地面的夾角分別是25°和60°,且AB=4米,求該生命跡象所在位置C的深度.(結(jié)果精確到1米.參考數(shù)據(jù):sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
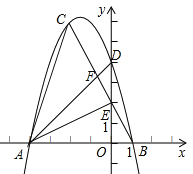
【題目】如圖,已知拋物線![]() 經(jīng)過點(diǎn)C(-2,6),
經(jīng)過點(diǎn)C(-2,6),
與x軸相交于A、B兩點(diǎn)(A在B的左側(cè)),與y軸交于點(diǎn)D.
(1)求點(diǎn)A的坐標(biāo);
(2)設(shè)直線BC交y軸于點(diǎn)E,連接AE、AC,求證:![]() 是等腰直角三角形;
是等腰直角三角形;
(3)連接AD交BC于點(diǎn)F,試問當(dāng)![]() 時,在拋物線上是否存在一點(diǎn)P使得以A、B、P為頂點(diǎn)的三角形與
時,在拋物線上是否存在一點(diǎn)P使得以A、B、P為頂點(diǎn)的三角形與![]() 相似?若存在, 請求出點(diǎn)P的坐標(biāo);若不存在,請說明理由.
相似?若存在, 請求出點(diǎn)P的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】按科學(xué)記算器MODE MODE 1,使顯示器顯示D后,求sin90°的值,以下按鍵順序正確的是( )
A.sin , 9=
B.9,sin=
C.sin , 9,0=
D.9,0=
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
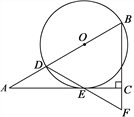
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=30°,點(diǎn)D在AB上,以BD為直徑的⊙O切AC于點(diǎn)E,連接DE并延長,交BC的延長線于點(diǎn)F.
(1)求證:△BDF是等邊三角形;
(2)連接AF、DC,若BC=3,寫出求四邊形AFCD面積的思路.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com