
【題目】如圖,一次函數(shù)y1=﹣x﹣1的圖象與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,與反比例函數(shù)![]() 圖象的一個(gè)交點(diǎn)為M(﹣2,m).
圖象的一個(gè)交點(diǎn)為M(﹣2,m).
(1)求反比例函數(shù)的解析式;(2)求點(diǎn)B到直線OM的距離.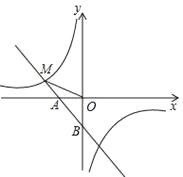
【答案】(1)![]() (2)
(2)![]()
【解析】
解:(1)∵一次函數(shù)y1=﹣x﹣1過M(﹣2,m),∴m=1。∴M(﹣2,1)。
把M(﹣2,1)代入![]() 得:k=﹣2。
得:k=﹣2。
∴反比列函數(shù)為![]() 。
。
(2)設(shè)點(diǎn)B到直線OM的距離為h,過M點(diǎn)作MC⊥y軸,垂足為C。
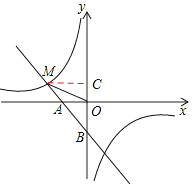
∵一次函數(shù)y1=﹣x﹣1與y軸交于點(diǎn)B,
∴點(diǎn)B的坐標(biāo)是(0,﹣1)。
∴![]() 。
。
在Rt△OMC中,![]() ,
,
∵![]() ,∴
,∴![]() 。
。
∴點(diǎn)B到直線OM的距離為![]() .
.
(1)根據(jù)一次函數(shù)解析式求出M點(diǎn)的坐標(biāo),再把M點(diǎn)的坐標(biāo)代入反比例函數(shù)解析式即可。
(2)設(shè)點(diǎn)B到直線OM的距離為h,過M點(diǎn)作MC⊥y軸,垂足為C,根據(jù)一次函數(shù)解析式表示出B點(diǎn)坐標(biāo),利用△OMB的面積=![]() ×BO×MC算出面積,利用勾股定理算出MO的長(zhǎng),再次利用三角形的面積公式可得
×BO×MC算出面積,利用勾股定理算出MO的長(zhǎng),再次利用三角形的面積公式可得![]() OMh,根據(jù)前面算的三角形面積可算出h的值
OMh,根據(jù)前面算的三角形面積可算出h的值


 A加金題 系列答案
A加金題 系列答案 全優(yōu)測(cè)試卷系列答案
全優(yōu)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二元一次方程![]() ,通過列舉將方程的解寫成下列表格的形式:
,通過列舉將方程的解寫成下列表格的形式:
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果將二元一次方程的解所包含的未知數(shù)![]() 的值對(duì)應(yīng)直角坐標(biāo)系中一個(gè)點(diǎn)的橫坐標(biāo),未知數(shù)
的值對(duì)應(yīng)直角坐標(biāo)系中一個(gè)點(diǎn)的橫坐標(biāo),未知數(shù)![]() 的值對(duì)應(yīng)這個(gè)點(diǎn)的縱坐標(biāo),這樣每一個(gè)二元一次方程的解,就可以對(duì)應(yīng)直角坐標(biāo)系中的一個(gè)點(diǎn),例如:方程
的值對(duì)應(yīng)這個(gè)點(diǎn)的縱坐標(biāo),這樣每一個(gè)二元一次方程的解,就可以對(duì)應(yīng)直角坐標(biāo)系中的一個(gè)點(diǎn),例如:方程![]() 的解
的解![]() 的對(duì)應(yīng)點(diǎn)是
的對(duì)應(yīng)點(diǎn)是![]() .
.
(1)表格中的![]() ________,
________,![]() ___________;
___________;
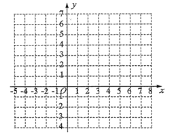
(2)通過以上確定對(duì)應(yīng)點(diǎn)坐標(biāo)的方法,將表格中給出的五個(gè)解依次轉(zhuǎn)化為對(duì)應(yīng)點(diǎn)的坐標(biāo),并在所給的直角坐標(biāo)系中畫出這五個(gè)點(diǎn);根據(jù)這些點(diǎn)猜想方程![]() 的解的對(duì)應(yīng)點(diǎn)所組成的圖形是_________,并寫出它的兩個(gè)特征①__________,②_____________;
的解的對(duì)應(yīng)點(diǎn)所組成的圖形是_________,并寫出它的兩個(gè)特征①__________,②_____________;
(3)若點(diǎn)![]() 好落在
好落在![]() 的解對(duì)應(yīng)的點(diǎn)組成的圖形上,求
的解對(duì)應(yīng)的點(diǎn)組成的圖形上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了提高服務(wù)質(zhì)量,某賓館決定對(duì)甲、乙兩種套房進(jìn)行星級(jí)提升,已知甲種套房提升費(fèi)用比乙種套房提升費(fèi)用少3萬(wàn)元,如果提升相同數(shù)量的套房,甲種套房費(fèi)用為625萬(wàn)元,乙種套房費(fèi)用為700萬(wàn)元.
(1)甲、乙兩種套房每套提升費(fèi)用各多少萬(wàn)元?
(2)如果需要甲、乙兩種套房共80套,市政府籌資金不少于2090萬(wàn)元,但不超過2096萬(wàn)元,且所籌資金全部用于甲、乙種套房星級(jí)提升,市政府對(duì)兩種套房的提升有幾種方案?哪一種方案的提升費(fèi)用最少?
(3)在(2)的條件下,根據(jù)市場(chǎng)調(diào)查,每套乙種套房的提升費(fèi)用不會(huì)改變,每套甲種套房提升費(fèi)用將會(huì)提高a萬(wàn)元(a>0),市政府如何確定方案才能使費(fèi)用最少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
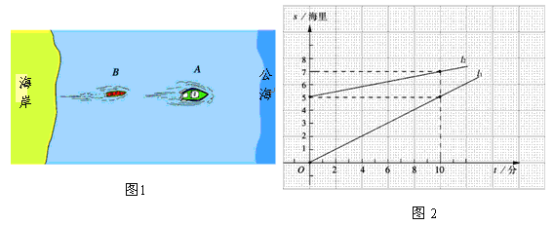
【題目】我國(guó)邊防局接到情報(bào),近海處有一可疑船只![]() 正向公海方向行駛,邊防部迅速派出快艇
正向公海方向行駛,邊防部迅速派出快艇![]() 追趕(如圖1) .圖2中
追趕(如圖1) .圖2中![]() 分別表示兩船相對(duì)于海岸的距離
分別表示兩船相對(duì)于海岸的距離![]() (海里)與追趕時(shí)間
(海里)與追趕時(shí)間![]() (分)之間的關(guān)系.根據(jù)圖象問答問題:
(分)之間的關(guān)系.根據(jù)圖象問答問題:
(1)①直線![]() 與直線
與直線![]() 中 表示
中 表示![]() 到海岸的距離與追趕時(shí)間之間的關(guān)系;
到海岸的距離與追趕時(shí)間之間的關(guān)系;
②![]() 與
與![]() 比較 速度快;
比較 速度快;
③如果一直追下去,那么![]() ________ (填 “能”或“不能")追上
________ (填 “能”或“不能")追上![]() ;
;
④可疑船只![]() 速度是 海里/分,快艇
速度是 海里/分,快艇![]() 的速度是 海里/分;
的速度是 海里/分;
(2)![]() 與
與![]() 對(duì)應(yīng)的兩個(gè)一次函數(shù)表達(dá)式
對(duì)應(yīng)的兩個(gè)一次函數(shù)表達(dá)式![]() 與
與![]() 中
中![]() 的實(shí)際意義各是什么?并直接寫出兩個(gè)具體表達(dá)式.
的實(shí)際意義各是什么?并直接寫出兩個(gè)具體表達(dá)式.
(3)![]() 分鐘內(nèi)
分鐘內(nèi)![]() 能否追上
能否追上![]() ?為什么?
?為什么?
(4)當(dāng)![]() 逃離海岸
逃離海岸![]() 海里的公海時(shí),
海里的公海時(shí), 將無法對(duì)其進(jìn)行檢查,照此速度,
將無法對(duì)其進(jìn)行檢查,照此速度,![]() 能否在
能否在![]() 逃入公海前將其攔截?為什么?
逃入公海前將其攔截?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊上一點(diǎn),連接BD,點(diǎn)
邊上一點(diǎn),連接BD,點(diǎn)![]() 為
為![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() ,
,![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)如圖2,若![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),求證:
的中點(diǎn),求證:![]() ;
;
(3)在(2)的條件下,如圖3,若![]() ,求線段
,求線段![]() 的長(zhǎng).
的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是等邊三角形,點(diǎn)
是等邊三角形,點(diǎn)![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 點(diǎn)在射線
點(diǎn)在射線![]() 上,
上,![]() 點(diǎn)在射線
點(diǎn)在射線![]() 上,
上,![]() ,
,
(1)如圖1,若![]() 點(diǎn)與點(diǎn)
點(diǎn)與點(diǎn)![]() 重合,求證:
重合,求證:![]() .
.
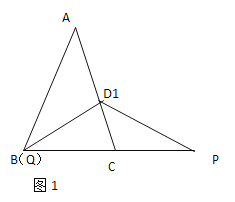
(2)如圖2,若點(diǎn)![]() 在線段
在線段![]() 上,點(diǎn)
上,點(diǎn)![]() 在線段
在線段![]() 上,
上,![]() 求
求![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
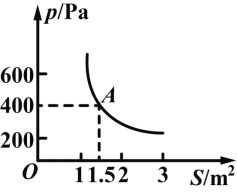
【題目】某科技小組進(jìn)行野外考察,途中遇到一片十幾米寬的泥地,他們沿著前進(jìn)路線鋪了若干塊木板,構(gòu)成一條臨時(shí)近道,木板對(duì)地面的壓強(qiáng)p(Pa)是木板面積S(m2)的反比例函數(shù),其圖象如圖所示.
(1)寫出這一函數(shù)的關(guān)系式和自變量的取值范圍.
(2)當(dāng)木板面積為0.2m2時(shí),壓強(qiáng)是多少?
(3)如果要求壓強(qiáng)不超過6000Pa,那么木板的面積至少為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,![]() 兩點(diǎn)的坐標(biāo)分別是點(diǎn)
兩點(diǎn)的坐標(biāo)分別是點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,且
,且![]() 滿足:
滿足:![]() .
.
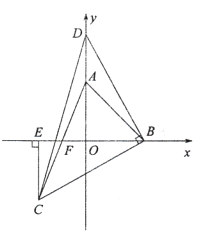
(1)求![]() 的度數(shù);
的度數(shù);
(2)點(diǎn)![]() 是
是![]() 軸正半軸上
軸正半軸上![]() 點(diǎn)上方一點(diǎn)(不與
點(diǎn)上方一點(diǎn)(不與![]() 點(diǎn)重合),以
點(diǎn)重合),以![]() 為腰作等腰
為腰作等腰![]() ,
,![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() .
.
①求證:![]() ;
;
②連接![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,若
,若![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
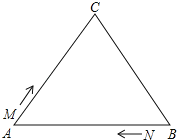
【題目】如圖,![]() 中,
中,![]() ,現(xiàn)有兩點(diǎn)
,現(xiàn)有兩點(diǎn)![]() 、
、![]() 分別從點(diǎn)A、點(diǎn)B同時(shí)出發(fā),沿三角形的邊運(yùn)動(dòng),已知點(diǎn)M的速度為1cm/s,點(diǎn)N的速度為2 cm/s.當(dāng)點(diǎn)N第一次到達(dá)B點(diǎn)時(shí),
分別從點(diǎn)A、點(diǎn)B同時(shí)出發(fā),沿三角形的邊運(yùn)動(dòng),已知點(diǎn)M的速度為1cm/s,點(diǎn)N的速度為2 cm/s.當(dāng)點(diǎn)N第一次到達(dá)B點(diǎn)時(shí),![]() 、
、![]() 同時(shí)停止運(yùn)動(dòng).
同時(shí)停止運(yùn)動(dòng).
(1)點(diǎn)![]() 、
、![]() 運(yùn)動(dòng)幾秒時(shí),
運(yùn)動(dòng)幾秒時(shí),![]() 、
、![]() 兩點(diǎn)重合?
兩點(diǎn)重合?
(2)點(diǎn)![]() 、
、![]() 運(yùn)動(dòng)幾秒時(shí),可得到等邊三角形
運(yùn)動(dòng)幾秒時(shí),可得到等邊三角形![]() ?
?
(3)當(dāng)點(diǎn)![]() 、
、![]() 在BC邊上運(yùn)動(dòng)時(shí),能否得到以MN為底邊的等腰三角形AMN?如存在,請(qǐng)求出此時(shí)
在BC邊上運(yùn)動(dòng)時(shí),能否得到以MN為底邊的等腰三角形AMN?如存在,請(qǐng)求出此時(shí)![]() 、
、![]() 運(yùn)動(dòng)的時(shí)間.
運(yùn)動(dòng)的時(shí)間.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com