
【題目】對于平面直角坐標(biāo)系xOy中的點(diǎn)M和圖形W1,W2給出如下定義:點(diǎn)P為圖形W1上一點(diǎn),點(diǎn)Q為圖形W2上一點(diǎn),當(dāng)點(diǎn)M是線段PQ的中點(diǎn)時,稱點(diǎn)M是圖形W1,W2的“中立點(diǎn)”.如果點(diǎn)P(x1,y1),Q(x2,y2),那么“中立點(diǎn)”M的坐標(biāo)為(![]() ,
,![]() ).
).
已知,點(diǎn)A(-3,0),B(0,4),C(4,0).
(1)連接BC,在點(diǎn)D(![]() ,0),E(0,1),F(0,
,0),E(0,1),F(0,![]() )中,可以成為點(diǎn)A和線段BC的“中立點(diǎn)”的是______;
)中,可以成為點(diǎn)A和線段BC的“中立點(diǎn)”的是______;
(2)已知點(diǎn)G(3,0),⊙G的半徑為2,如果直線y=-x+1存在點(diǎn)K可以成為點(diǎn)A和⊙G的“中立點(diǎn)”,求點(diǎn)K的坐標(biāo);
(3)以點(diǎn)C為圓心,半徑為2作圓,點(diǎn)N為直線y=2x+4上的一點(diǎn),如果存在點(diǎn)N,使得y軸上的一點(diǎn)可以成為點(diǎn)N與⊙C的“中立點(diǎn)”,直接寫出點(diǎn)N的橫坐標(biāo)的取值范圍.
【答案】(1)D、F;(2)點(diǎn)K坐標(biāo)為(1,0)或(0,1);(3)-6≤xN≤-2
【解析】
(1)根據(jù)新定義,點(diǎn)A和線段BC的“中立點(diǎn)”是點(diǎn)D、F;
(2)點(diǎn)A和⊙G的“中立點(diǎn)”在以點(diǎn)O為圓心、半徑為1的圓上運(yùn)動,因為點(diǎn)K在直線y=-x+1上,設(shè)出點(diǎn)K坐標(biāo),求解即可;
(3)根據(jù)題意可得,點(diǎn)N與圓C的“中立點(diǎn)”在以線段NC的中點(diǎn)P為圓心、半徑為1的圓上運(yùn)動,⊙P與y軸相切時,即可求得其取值范圍.
(1)如圖1中,
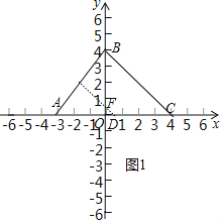
觀察圖象可知,滿足條件的點(diǎn)在△ABC的平行于BCD的中位線上,
故成為點(diǎn)A和線段BC的“中立點(diǎn)”的是D、F.
故答案為D、F;
(2)如圖2中,點(diǎn)A和⊙G的“中立點(diǎn)”在以O為圓心,1為半徑的圓上運(yùn)動,
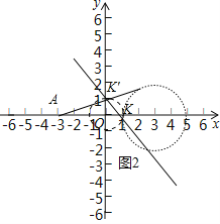
因為點(diǎn)K在直線y=-x+1上,設(shè)K(m,-m+1),
則有m2+(-m+1)2=1,
解得m=0或1,
∴點(diǎn)K坐標(biāo)為(1,0)或(0,1).
(3)如圖3中,由題意,當(dāng)點(diǎn)N確定時,點(diǎn)N與⊙G的“中立點(diǎn)”是以NC的中點(diǎn)P為圓心1為半徑的⊙P,
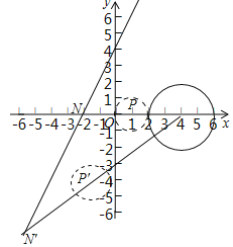
當(dāng)⊙P與y軸相切時,點(diǎn)N的橫坐標(biāo)分別為-2或-6,
所以滿足條件的點(diǎn)N的橫坐標(biāo)的取值范圍為-6≤xN≤-2.


 作業(yè)輔導(dǎo)系列答案
作業(yè)輔導(dǎo)系列答案 同步學(xué)典一課多練系列答案
同步學(xué)典一課多練系列答案 經(jīng)典密卷系列答案
經(jīng)典密卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某食品廠生產(chǎn)一種半成品食材,成本為2元/千克,每天的產(chǎn)量P(百千克)與銷售價格x(元/千克)滿足函數(shù)關(guān)系式p=![]() x+8.從市場反饋的信息發(fā)現(xiàn),該食材每天的市場需求量q(百千克)與銷售價格x(元/千克)滿足一次函數(shù)關(guān)系,部分?jǐn)?shù)據(jù)如表:
x+8.從市場反饋的信息發(fā)現(xiàn),該食材每天的市場需求量q(百千克)與銷售價格x(元/千克)滿足一次函數(shù)關(guān)系,部分?jǐn)?shù)據(jù)如表:
銷售價格x(元/千克) | 2 | 4 | …… | 10 |
市場需求量q(百千克) | 12 | 10 | …… | 4 |
已知按物價部門規(guī)定銷售價格x不低于2元/千克且不高于10元/千克,
(1)直接寫出q與x的函數(shù)關(guān)系式,并注明自變量x的取值范圍;
(2)當(dāng)每天的產(chǎn)量小于或等于市場需求量時,這種食材能全部售出;當(dāng)每天的產(chǎn)量大于市場需求量時,只能售出市場需求的量,而剩余的食材由于保質(zhì)期短作廢棄處理;
①當(dāng)每天的食材能全部售出時,求x的取值范圍;
②求廠家每天獲得的利潤y(百元)與銷售價格x的函數(shù)關(guān)系式;
(3)在(2)的條件下,當(dāng)x為多少時,y有最大值,并求出最大利潤.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在邊
在邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在四邊形
在四邊形![]() 內(nèi)部且到邊
內(nèi)部且到邊![]() 、
、![]() 的距離相等,若要使
的距離相等,若要使![]() 是直角三角形且
是直角三角形且![]() 是等腰三角形,則
是等腰三角形,則![]() __________.
__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)A的坐標(biāo)為(2,1),如果將線段OA繞點(diǎn)O逆時針方向旋轉(zhuǎn)90°,那么點(diǎn)A的對應(yīng)點(diǎn)的坐標(biāo)為( )

A. (﹣1,2) B. (﹣2,1) C. (1,﹣2) D. (2,﹣1)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
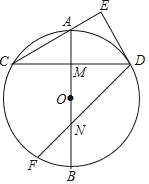
【題目】如圖,AB是⊙O的直徑,M是OA的中點(diǎn),弦CD⊥AB于點(diǎn)M,過點(diǎn)D作DE⊥CA交CA的延長線于點(diǎn)E.
(1)連接AD,則∠OAD= °;
(2)求證:DE與⊙O相切;
(3)點(diǎn)F在![]() 上,∠CDF=45°,DF交AB于點(diǎn)N.若DE=3,求FN的長.
上,∠CDF=45°,DF交AB于點(diǎn)N.若DE=3,求FN的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=AC,DE∥BC,點(diǎn)F在邊AC上,DF與BE相交于點(diǎn)G,且∠EDF=∠ABE.
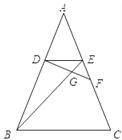
求證:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰三角形ABC中,當(dāng)頂角∠A的大小確定時,它的對邊(即底邊BC)與鄰邊(即腰AB或AC)的比值也就確定,我們把這個比值記作T(A),即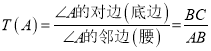 ,如T(60°)=1.
,如T(60°)=1.
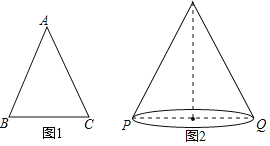
(1)理解鞏固:T(90°)= ,T(120°)= ;
(2)學(xué)以致用:如圖2,圓錐的母線長為9,底面直徑PQ=8,一只螞蟻從P點(diǎn)這沿著圓錐的側(cè)面爬行到點(diǎn)Q.
①求圓錐側(cè)面展開圖的扇形圓心角的數(shù);
②求螞蟻爬行的最短路徑長(精確到0.1).(參考數(shù)據(jù):T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
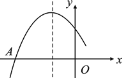
【題目】如圖是二次函數(shù)y=ax2+bx+c圖象的一部分,圖象過點(diǎn)A(-3,0),對稱軸為直線x=-1,給出四個結(jié)論:①c>0;② 2a-b=0;③![]() <0;④若點(diǎn)
<0;④若點(diǎn)![]() 為函數(shù)圖象上的兩點(diǎn),則y1<y2,其中,正確結(jié)論的個數(shù)是( )
為函數(shù)圖象上的兩點(diǎn),則y1<y2,其中,正確結(jié)論的個數(shù)是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了豐富同學(xué)們的知識,拓展閱讀視野,學(xué)習(xí)圖書館購買了一些科技、文學(xué)、歷史等書籍,進(jìn)行組合搭配成![]() 、
、![]() 、
、![]() 三種套型書籍,發(fā)放給各班級的圖書角供同學(xué)們閱讀,已知各套型的規(guī)格與價格如下表:
三種套型書籍,發(fā)放給各班級的圖書角供同學(xué)們閱讀,已知各套型的規(guī)格與價格如下表:
|
|
| |
規(guī)格(本/套) | 12 | 9 | 7 |
價格(元/套) | 200 | 150 | 120 |
(1)已知搭配![]() 、
、![]() 兩種套型書籍共15套,需購買書籍的花費(fèi)是2120元,問
兩種套型書籍共15套,需購買書籍的花費(fèi)是2120元,問![]() 、
、![]() 兩種套型各多少套?
兩種套型各多少套?
(2)若圖書館用來搭配的書籍共有2100本,現(xiàn)將其搭配成![]() 、
、![]() 兩種套型書籍,這兩種套型的總價為30750元,求搭配后剩余多少本書?
兩種套型書籍,這兩種套型的總價為30750元,求搭配后剩余多少本書?
(3)若圖書館用來搭配的書籍共有122本,現(xiàn)將其搭配成![]() 、
、![]() 、
、![]() 三種套型書籍共13套,且沒有剩余,請求出所有搭配的方案.
三種套型書籍共13套,且沒有剩余,請求出所有搭配的方案.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com