
已知△ABC中,∠C是其最小的內角,如果過頂點B的一條直線把這個三角形分割成了兩個三角形,其中一個為等腰三角形,另一個為直角三角形,則稱這條直線為△ABC的關于點B的伴侶分割線.例如:如圖1,在Rt△ABC中,∠C=20°,過頂點B的一條直線BD交AC于點D,且∠DBC=20°,顯然直線BD是△ABC的關于點B的伴侶分割線.
(1)如圖2,在△ABC中,∠C=20°,∠ABC=110°.請在圖中畫出△ABC的關于點B 的伴侶分割線,并標注角度;
(2)在△ABC中,設∠B的度數為y,最小內角∠C的度數為x.試探索y與x之間滿足怎樣的關系時,△ABC存在關于點B的伴侶分割線.
解:(1)畫圖正確,角度標注 正確
正確
(2)設BD為△ABC的伴侶分割線,分以下兩種情況.
第一種情況:△BDC是等腰三角形,△ABD是直角三角形,
易知∠C和∠DBC必為底角,∴ ∠DBC=∠C=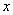 .
.
當∠A=90°時,△ABC存在伴侶分割線,此時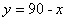 ,
,
當∠ABD=90°時,△ABC存在伴侶分割線,此時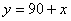 ,
,
當∠ADB=90°時,△ABC存在伴侶分割線,此時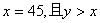 ;
;
第二種情況:△BDC是直角三角形,△ABD是等腰三角形,
當∠DBC=90°時,若BD=AD,則△ABC存在伴侶分割線,
此時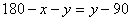 ,∴
,∴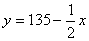 ,
,
當∠BDC=90°時,若BD=AD,則△ABC存在伴侶分割線,
此時∠A=45°,∴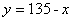 .
.
綜上所述,當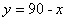 或
或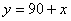 或
或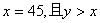 或
或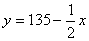 或
或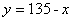 時△ABC存在伴侶分割線.
時△ABC存在伴侶分割線.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:初中數學 來源: 題型:
(1)甲、乙、丙三只不透明的口袋中都裝有1個白球、1個紅球,它們除顏色外都相同,攪勻后分別從三只口袋中任意摸出1個球,求從三只口袋摸出的都是紅球的概率.
(2)甲、乙、丙、丁四位同學分別站在正方形場地的四個頂點A、B、C、D處,每個人都以相同的速度沿著正方形的邊同時出發隨機走向相鄰的頂點處,那么甲、乙、丙、丁四位同學互不相遇的概率是 .① 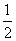 ②
② 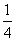 ③
③ 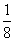
 ④
④ 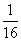
查看答案和解析>>
科目:初中數學 來源: 題型:
若正比例函數y=2x與反比例 函數y=
函數y=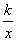 (k≠0)的圖像相交,則當x<0時,交點位于( )
(k≠0)的圖像相交,則當x<0時,交點位于( )
|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中數學 來源: 題型:
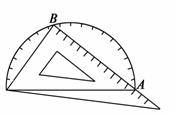
小聰有一塊含有30°角的直角三角板,他想只利用量角器來測量較短直角邊的長度,于是他采用如圖的方法,小聰發現點A處的三角板讀數為12cm,點B處的量角器的讀數為74°,由此可知三角板的較短直角邊的長度約為 cm.(參考數據:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,將一條長為60 cm的卷尺鋪平后折疊,使得卷尺自身的一部分重合,然后在重合部分(陰影處)沿與卷尺邊 垂直的方向剪一刀,此時卷尺分為了三段,若這三段長度由短到長的比為1︰2︰3,則折痕對應的刻度有
垂直的方向剪一刀,此時卷尺分為了三段,若這三段長度由短到長的比為1︰2︰3,則折痕對應的刻度有  ▲ 種可能.
▲ 種可能.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com