
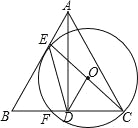
【題目】如圖,在△ABC中,AB=AC,AD⊥BC于點D,E為邊AB上一點,ED=CD,以CE為直徑作⊙O,交BC于點F.
(1)求證:AB與⊙O相切;
(2)若DF=1,DC=3,求AE的長.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)根據等腰三角形的性質,由AB=AC,AD⊥BC得到BD=CD,則可判斷OD為△BCE的中位線,所以OD∥BE,再根據等腰三角形的性質,由DE=DC,OE=OC得到DO⊥CE,則BE⊥CE,于是根據切線的性質可判斷AB與⊙O相切;
(2)連結EF,如圖,根據圓周角定理得∠EFC=90°,在Rt△DEF中利用勾股定理計算出EF=2![]() ,再在Rt△BEF中利用勾股定理計算出BE=2
,再在Rt△BEF中利用勾股定理計算出BE=2![]() ,然后根據平行線分線段成比例定理可求出AE的長.
,然后根據平行線分線段成比例定理可求出AE的長.
試題解析:(1)∵AB=AC,AD⊥BC,
∴BD=CD,
∵OE=OC,
∴OD為△BCE的中位線,
∴OD∥BE,
∵DE=DC,OE=OC,
∴DO⊥CE,
∴BE⊥CE,
∴AB與⊙O相切;
(2)連結EF,如圖,
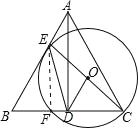
∵CE為⊙O的直徑,
∴∠EFC=90°,
在Rt△DEF中,∵DE=DC=3,DF=1,
∴EF=![]() ,
,
∵DB=DC=3,
∴BF=BD-DF=3-1=2,
在Rt△BEF中,∵EF=2![]() ,BF=2,
,BF=2,
∴BE=![]() ,
,
∵EF∥AD,
∴![]() ,即
,即![]() ,
,
∴AE=![]() .
.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
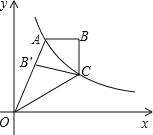
【題目】如圖,雙曲線y=![]() (x>0)經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與x軸正半軸的夾角,AB∥x軸.將△ABC沿AC翻折后得△AB′C,B′點落在OA上,則四邊形OABC的面積是 .
(x>0)經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與x軸正半軸的夾角,AB∥x軸.將△ABC沿AC翻折后得△AB′C,B′點落在OA上,則四邊形OABC的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
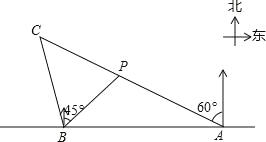
【題目】如圖,在筆直的海岸線l上有A、B兩個觀測站,A在B的正東方向,AB=(![]() +1)km,小船在點P處,從A測得小船在北偏西60°的方向,從B測得小船在北偏東45°方向.
+1)km,小船在點P處,從A測得小船在北偏西60°的方向,從B測得小船在北偏東45°方向.
(1)求點P到海岸線l的距離;
(2)小船從點P處沿射線AP的方向航行一段時間后,到達點C處,此時,從B測得小船在北偏西15°的方向,求點C與點B之間的距離.(友情提示:結果都保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
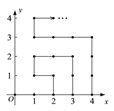
【題目】如圖,在平面直角坐標系中,有若干個橫縱坐標分別為整數的點,其順序為(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根據這個規律,第2016個點的坐標為( )
A(45,9) B(45,13) C(45,22) D(45,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】麒麟區是云南省曲靖市政府所在地,位于云南省東部,滇東高原中部,南盤江上游,截止2018年末麒麟區有常住人口約76萬人,76萬這個數字用科學記數法表示為( )
A. 0.76×106B. 7.6×105C. 76×104D. 7.6×106
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】方程x2+px+q=0,甲同學因為看錯了常數項,解得的根是6,-1;乙同學看錯了一次項,解得的根是-2,-3,則原方程為_______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com