
【題目】已知,如圖,線段AB,利用無刻度的直尺和圓規(guī),作一個滿足條件的△ABC:①△ABC為直角三角形;②tan∠A= ![]() .(注:不要求寫作法,但保留作圖痕跡)
.(注:不要求寫作法,但保留作圖痕跡)![]()
【答案】解:①如圖,延長AB至M,使得AM=3AB;
②過點M作MN⊥AB,且截取MN=AB,連接AN;
③過點B作AB的垂線,交AN于點C.

∴Rt△ABC即為所求
【解析】通過作垂線,構(gòu)造一個直角三角形,把∠A放到這個三角形中,再過B 作垂線構(gòu)造與前一個相似的三角形,可作出滿足條件的三角形.
【考點精析】根據(jù)題目的已知條件,利用解直角三角形的相關(guān)知識可以得到問題的答案,需要掌握解直角三角形的依據(jù):①邊的關(guān)系a2+b2=c2;②角的關(guān)系:A+B=90°;③邊角關(guān)系:三角函數(shù)的定義.(注意:盡量避免使用中間數(shù)據(jù)和除法).


 53隨堂測系列答案
53隨堂測系列答案科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 為
為![]() 軸上的動點,點
軸上的動點,點![]() 為
為![]() 軸上方的動點,連接
軸上方的動點,連接![]() ,
,![]() ,
,![]() .
.
(1)如圖1,當點![]() 在
在![]() 軸上,且滿足
軸上,且滿足![]() 的角平分線與
的角平分線與![]() 的角平分線交于點
的角平分線交于點![]() ,請直接寫出
,請直接寫出![]() 的度數(shù);
的度數(shù);

(2)如圖2,當點![]() 在
在![]() 軸上,
軸上,![]() 的角平分線與
的角平分線與![]() 的角平分線交于點
的角平分線交于點![]() ,點
,點![]() 在
在![]() 的延長線上,且滿足
的延長線上,且滿足![]() ,求
,求![]() ;
;

(3)如圖3,當點![]() 在第一象限內(nèi),點
在第一象限內(nèi),點![]() 是
是![]() 內(nèi)一點,點
內(nèi)一點,點![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 上一點,滿足:
上一點,滿足:![]() ,
,![]() ,
,![]() .
.

以下結(jié)論:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .
.
正確的是:________.(請?zhí)顚懻_結(jié)論序號,并選擇一個正確的結(jié)論證明,簡寫證明過程).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】根據(jù)下列證明過程填空

如圖,因為∠A=_____(已知),
所以AC∥ED( )
因為∠2=_____(已知),
所以AC∥ED( )
因為∠A+_____=180°(已知),
所以AB∥FD( )
因為AB∥_____(已知),
所以∠2+∠AED=180°( )
因為AC∥_____(已知),
所以∠C=∠3( )
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在2017年“KFC”籃球賽進校園活動中,某校甲、乙兩隊進行決賽,比賽規(guī)則規(guī)定:兩隊之間進行3局比賽,3局比賽必須全部打完,只要贏滿2局的隊為獲勝隊,假如甲、乙兩隊之間每局比賽輸贏的機會相同,且乙隊已經(jīng)贏得了第1局比賽,那么甲隊獲勝的概率是多少?(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中;長方形ABCD的四個頂點分別為
中;長方形ABCD的四個頂點分別為![]() ;
;![]() ,
,![]() ,
,![]() .對該長方形及其內(nèi)部的每一個點都進行如下操作:把每個點的橫坐標都乘以同一個實數(shù)
.對該長方形及其內(nèi)部的每一個點都進行如下操作:把每個點的橫坐標都乘以同一個實數(shù)![]() ,縱坐標都乘以3,再將得到的點向右平移
,縱坐標都乘以3,再將得到的點向右平移![]() 個單位,向下平移
個單位,向下平移![]() 個單位,得到長方形
個單位,得到長方形![]() 及其內(nèi)部的點,其中點
及其內(nèi)部的點,其中點![]() ,
,![]() ,
,![]() ,
,![]() 的對應(yīng)點分別為A’,B’,C’,D’,
的對應(yīng)點分別為A’,B’,C’,D’,
(1)點A’的橫坐標為______(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)若點A’的坐標為![]() ,點C’的坐標為
,點C’的坐標為![]() ,求
,求![]() ,
,![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
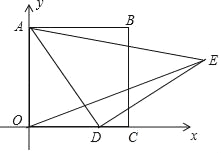
【題目】如圖,在平面直角坐標系中,已知正方形ABCO,A(0,3),點D為x軸上一動點,以AD為邊在AD的右側(cè)作等腰Rt△ADE,∠ADE=90°,連接OE,則OE的最小值為( )
A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了解我校七年級![]() 名學生的體重情況,現(xiàn)從中隨機抽取
名學生的體重情況,現(xiàn)從中隨機抽取![]() 名學生測量體重進行統(tǒng)計分析,關(guān)于本次調(diào)查下列說法正確的是( )
名學生測量體重進行統(tǒng)計分析,關(guān)于本次調(diào)查下列說法正確的是( )
A.本次調(diào)查中的總體是七年級![]() 名學生
名學生
B.本次調(diào)查中的樣本是隨機抽取的![]() 名學生的體重
名學生的體重
C.本次調(diào)查中的樣本容量是![]() 名
名
D.本次調(diào)查中的個體是七年級的每個學生
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
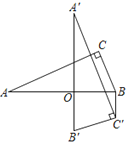
【題目】如圖,在Rt△ABC中,∠C=90°,AC=12,BC=5,將△ABC繞AB上的點O順時針旋轉(zhuǎn)90°,得到△A'B'C',連結(jié)BC'.若BC'∥A'B',則OB的值為( )
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com