
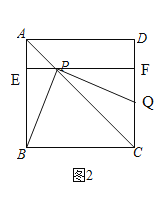
【題目】已知正方形![]() ,點(diǎn)
,點(diǎn)![]() 是其內(nèi)部一點(diǎn).
是其內(nèi)部一點(diǎn).

(1)如圖1,點(diǎn)![]() 在邊
在邊![]() 的垂直平分線
的垂直平分線![]() 上,將
上,將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn),得到
逆時(shí)針旋轉(zhuǎn),得到![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 落在
落在![]() 上時(shí),恰好點(diǎn)
上時(shí),恰好點(diǎn)![]() 落在直線
落在直線![]() 上,求
上,求![]() 的度數(shù);
的度數(shù);
(2)如圖2,點(diǎn)![]() 在對(duì)角線
在對(duì)角線![]() 上,連接
上,連接![]() ,若將線段
,若將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 后得到線段
后得到線段![]() ,試問(wèn)點(diǎn)
,試問(wèn)點(diǎn)![]() 是否在直線
是否在直線![]() 上,請(qǐng)給出結(jié)論,并說(shuō)明理由;
上,請(qǐng)給出結(jié)論,并說(shuō)明理由;
(3)如圖3,若![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,![]() ,請(qǐng)寫出
,請(qǐng)寫出![]() 、
、![]() 、
、![]() 這三條線段長(zhǎng)之間滿足的數(shù)量關(guān)系是____________.
這三條線段長(zhǎng)之間滿足的數(shù)量關(guān)系是____________.
【答案】(1)![]() ;(2)點(diǎn)
;(2)點(diǎn)![]() 在直線
在直線![]() 上,理由見(jiàn)解析;(3)
上,理由見(jiàn)解析;(3)![]()
【解析】
(1)根據(jù)中垂線的性質(zhì)和旋轉(zhuǎn)的性質(zhì)判定![]() 是等邊三角形,從而求解;
是等邊三角形,從而求解;
(2)根據(jù)題意證明∴![]() ,從而求證;
,從而求證;
(3)把△ABP繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)90°,繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°,根據(jù)旋轉(zhuǎn)變換只改變圖形的位置不改變圖形的形狀可得等腰直角三角形,根據(jù)等腰直角三角形的性質(zhì)和勾股定理得出結(jié)論,等量代換求解.
連接![]() ,
,
∵點(diǎn)![]() 在邊
在邊![]() 的垂直平分線
的垂直平分線![]() 上,
上,
∴![]() .
.
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

(2)點(diǎn)![]() 在直線
在直線![]() 上.證明如下:
上.證明如下:
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .
.
∴![]() ,
,
∴![]() ,
,![]()
∴![]()
又∵![]() 在正方形對(duì)角線
在正方形對(duì)角線![]() 上,∴∠EAP=∠APE=45°
上,∴∠EAP=∠APE=45°
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 8逆時(shí)針旋轉(zhuǎn)
8逆時(shí)針旋轉(zhuǎn)![]() 后得到線段
后得到線段![]() ,點(diǎn)
,點(diǎn)![]() 在直線
在直線![]() 上.
上.
(3)
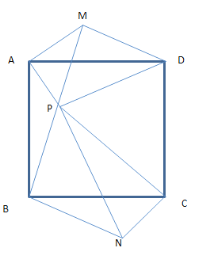
如圖,將△ABP繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)90°得到△AMD,
由題意可知:∠APB=∠AAMD=135°,DM=BP,AP=AM=a,∠PAM=90°
∴∠AMP=45°
∴∠PMD=90°
∴在Rt△APM中,![]()
在Rt△PMD中,![]()
∴![]()
將△ABP繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°得到△BNC,同理可證
在Rt△PNC中,![]()
在Rt△BPN中,![]()
∴![]()
所以可得:![]()
整理得:
![]() .
.


 學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案
學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】銅陵市義安區(qū)實(shí)施了城鄉(xiāng)居民基本醫(yī)療保險(xiǎn)(簡(jiǎn)稱“醫(yī)療保險(xiǎn)”),辦法規(guī)定農(nóng)村村民只要每人每年交納180元錢就可以加入醫(yī)療保險(xiǎn),住院時(shí)自己先墊付,出院同時(shí)就可得到按一定比例的報(bào)銷款,這項(xiàng)舉措惠及民生,吳斌與同學(xué)隨機(jī)調(diào)查了他們鎮(zhèn)的一些農(nóng)民,根據(jù)收集到的數(shù)據(jù)繪制了以下的統(tǒng)計(jì)圖.
根據(jù)圖中信息,解答下列問(wèn)題:
(1)本次調(diào)查了多少村民?被調(diào)查的村民中參加醫(yī)療保險(xiǎn),得到報(bào)銷款的有多少人?
(2)若該鎮(zhèn)有34000村民,請(qǐng)估算有多少人參加了醫(yī)療保險(xiǎn)?要使兩年后參加醫(yī)療保險(xiǎn)的人數(shù)增加到業(yè)務(wù)31460人,假設(shè)這兩年的年增長(zhǎng)率相同,求年增長(zhǎng)率?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀材料:為解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我們可以將x2﹣1視為一個(gè)整體,然后設(shè)x2﹣1=y,則(x2﹣1)2=y2,原方程化為y2﹣5y+4=0.
解得y1=1,y2=4
當(dāng)y=1時(shí),x2﹣1=1.∴x2=2.∴x=±![]() ;
;
當(dāng)y=4時(shí),x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解為x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() ,
,
請(qǐng)利用以上知識(shí)解決下列問(wèn)題:
如果(m2+n2﹣1)(m2+n2+2)=4,則m2+n2=__.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】江蘇是全國(guó)首個(gè)自然村“村村通寬帶”省份.我市某村為了將當(dāng)?shù)剞r(nóng)產(chǎn)品外銷,建立了淘寶網(wǎng)店.該網(wǎng)店于今年7月底以每袋25元的成本價(jià)收購(gòu)一批農(nóng)產(chǎn)品.當(dāng)商品售價(jià)為每袋40元時(shí),8月份銷售256袋.9、10月該商品十分暢銷.銷售量持續(xù)走高.在售價(jià)不變的基礎(chǔ)上,10月份的銷售量達(dá)到400袋.設(shè)9、10這兩個(gè)月月平均增長(zhǎng)率不變.
(1)求9、10這兩個(gè)月的月平均增長(zhǎng)率;
(2)為迎接雙“十一”,11月份起,該網(wǎng)店采用降價(jià)促銷的方式回饋顧客,經(jīng)調(diào)查發(fā)現(xiàn),該農(nóng)產(chǎn)品每降價(jià)1元/每袋,銷售量就增加5袋,當(dāng)農(nóng)產(chǎn)品每袋降價(jià)多少元時(shí),該淘寶網(wǎng)店11月份獲利4250元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 、
、![]() 為邊
為邊![]() 和
和![]() 上的動(dòng)點(diǎn)(不含端點(diǎn)),
上的動(dòng)點(diǎn)(不含端點(diǎn)),![]() .下列三個(gè)結(jié)論:①當(dāng)
.下列三個(gè)結(jié)論:①當(dāng)![]() 時(shí),則
時(shí),則![]() ;②
;②![]() ;③
;③![]() 的周長(zhǎng)不變,其中正確結(jié)論的個(gè)數(shù)是( )
的周長(zhǎng)不變,其中正確結(jié)論的個(gè)數(shù)是( )
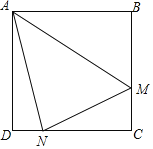
A.0B.1
C.2D.3
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一次中學(xué)生田徑運(yùn)動(dòng)會(huì)上,根據(jù)參加男子跳高初賽的運(yùn)動(dòng)員的成績(jī)(單位:m),繪制出如下的統(tǒng)計(jì)圖①和圖②,請(qǐng)根據(jù)相關(guān)信息,解答下列問(wèn)題:

(Ⅰ)圖1中a的值為 ;
(Ⅱ)求統(tǒng)計(jì)的這組初賽成績(jī)數(shù)據(jù)的平均數(shù)、眾數(shù)和中位數(shù);
(Ⅲ)根據(jù)這組初賽成績(jī),由高到低確定9人進(jìn)入復(fù)賽,請(qǐng)直接寫出初賽成績(jī)?yōu)?.65m的運(yùn)動(dòng)員能否進(jìn)入復(fù)賽.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5,AC=4,E、F分別為AB、BC上的點(diǎn),沿直線EF將∠B折疊,使點(diǎn)B恰好落在AC上的D處,當(dāng)△ADE恰好為直角三角形時(shí),BE的長(zhǎng)為_____.
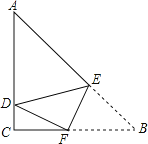
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是邊
是邊![]() 上一點(diǎn),
上一點(diǎn),![]() ,連接
,連接![]() .
.
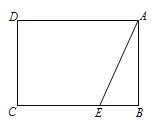
(1)沿![]() 翻折
翻折![]() 使點(diǎn)
使點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,
處,
①連接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②連接![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(2)![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)得
順時(shí)針旋轉(zhuǎn)得![]() ,點(diǎn)
,點(diǎn)![]() 落在邊
落在邊![]() 上時(shí)旋轉(zhuǎn)停止. 若點(diǎn)
上時(shí)旋轉(zhuǎn)停止. 若點(diǎn)![]() 落在矩形對(duì)角線
落在矩形對(duì)角線![]() 上,且點(diǎn)
上,且點(diǎn)![]() 到
到![]() 的距離小于
的距離小于![]() 時(shí),求
時(shí),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分別是AB,BC的中點(diǎn),則下列結(jié)論不一定正確的是( )
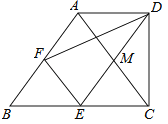
A.△ABC是等腰三角形B.四邊形EFAM是菱形
C.![]() D.DE平分∠CDF
D.DE平分∠CDF
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com