
【題目】如圖,平行四邊形ABCD中,AB=2,AD=4,對(duì)角線AC,BD相交于點(diǎn)O,且E,F,G,H分別是AO,BO,CO,DO的中點(diǎn),則下列說(shuō)法正確的是( )
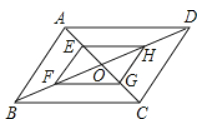
A.EH=HGB.四邊形EFGH是平行四邊形
C.AC⊥BDD.![]() 的面積是
的面積是![]() 的面積的2倍
的面積的2倍
【答案】B
【解析】
根據(jù)三角形中位線的性質(zhì)和平行四邊形的性質(zhì)分別判斷各選項(xiàng)即可解答,
解:因?yàn)?/span>E、H為OA、OD的中點(diǎn),
所以,EH=![]() =2,同理,HG=
=2,同理,HG=![]() =1,所以,A錯(cuò)誤;
=1,所以,A錯(cuò)誤;
EH∥AD,EH=![]() ,
,
FG∥BC,FG=![]() ,
,
因?yàn)槠叫兴倪呅?/span>ABCD中,AD=BC,且AD∥BC,
所以,EH=FG,且EH∥FG,
所以,四邊形EFGH是平行四邊形, B正確.
AC與BD不一定垂直,C錯(cuò)誤;
由相似三角形的面積比等于相似比的平方,知:△ABC的面積是△EFO的面積的4倍,D錯(cuò)誤;
故選B.


 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案 優(yōu)百分課時(shí)互動(dòng)系列答案
優(yōu)百分課時(shí)互動(dòng)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線y=x2﹣bx+2b(b是常數(shù)).
(1)無(wú)論b取何值,該拋物線都經(jīng)過(guò)定點(diǎn) D.請(qǐng)寫出點(diǎn)D的坐標(biāo).
(2)該拋物線的頂點(diǎn)是(m,n),當(dāng)b取不同的值時(shí),求n關(guān)于m的函數(shù)解析式.
(3)若在0≤x≤4的范圍內(nèi),至少存在一個(gè)x的值,使y<0,求b的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】正方形![]() 、
、![]() 、
、![]() 、…按如圖所示的方式放置.點(diǎn)
、…按如圖所示的方式放置.點(diǎn)![]() 、
、![]() 、
、![]() 、…和點(diǎn)
、…和點(diǎn)![]() 、
、![]() 、
、![]() 、…分別在直線
、…分別在直線![]() 和
和![]() 軸上,則點(diǎn)
軸上,則點(diǎn)![]() 的坐標(biāo)是__________.(
的坐標(biāo)是__________.(![]() 為正整數(shù))
為正整數(shù))

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
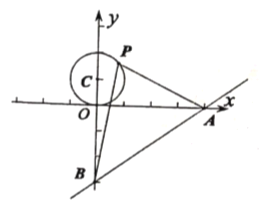
【題目】如圖,已知直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() 是以
是以![]() 為圓心,1為半徑的圓上一動(dòng)點(diǎn),連接
為圓心,1為半徑的圓上一動(dòng)點(diǎn),連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 的面積最大時(shí),點(diǎn)
的面積最大時(shí),點(diǎn)![]() 的坐標(biāo)為__________.
的坐標(biāo)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了“城市更美好、人民更幸福”,我市開展“三城聯(lián)創(chuàng)”活動(dòng),環(huán)衛(wèi)部門要求垃圾按![]() 三類分別裝袋、投放,其中
三類分別裝袋、投放,其中![]() 類指廢電池,過(guò)期藥品等有毒垃圾,
類指廢電池,過(guò)期藥品等有毒垃圾,![]() 類指剩余食品等廚余垃圾,
類指剩余食品等廚余垃圾,![]() 類指塑料、廢紙等可回收垃圾,甲、乙兩人各投放一袋垃圾.
類指塑料、廢紙等可回收垃圾,甲、乙兩人各投放一袋垃圾.
(1)甲投放的垃圾恰好是![]() 類的概率是 ;
類的概率是 ;
(2)用樹狀圖或表格求甲、乙兩人投放的垃圾是不同類別的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
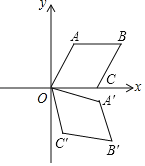
【題目】如圖,在平面直角坐標(biāo)系xOy中,菱形OABC的邊長(zhǎng)為2,點(diǎn)A在第一象限,點(diǎn)C在x軸正半軸上,∠AOC=60°,若將菱形OABC繞點(diǎn)O順時(shí)針旋轉(zhuǎn)75°,得到四邊形OA′B′C′,則點(diǎn)B的對(duì)應(yīng)點(diǎn)B′的坐標(biāo)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
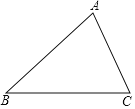
【題目】如圖,已知△ABC中,AB=BC=5,tan∠ABC=![]() .
.
(1)求邊AC的長(zhǎng);
(2)設(shè)邊BC的垂直平分線與邊AB的交點(diǎn)為D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系![]() 中,函數(shù)
中,函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() ,
,![]() )的圖象經(jīng)過(guò)點(diǎn)
)的圖象經(jīng)過(guò)點(diǎn)![]() 和
和![]() ,直線
,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點(diǎn).
兩點(diǎn).
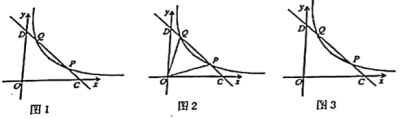
(1)求![]() 的度數(shù);
的度數(shù);
(2)如圖2,連接![]() 、
、![]() ,當(dāng)
,當(dāng)![]() 時(shí),求此時(shí)
時(shí),求此時(shí)![]() 的值:
的值:
(3)如圖3,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 分別在
分別在![]() 軸和
軸和![]() 軸正半軸上的動(dòng)點(diǎn).再以
軸正半軸上的動(dòng)點(diǎn).再以![]() 、
、![]() 為鄰邊作矩形
為鄰邊作矩形![]() .若點(diǎn)
.若點(diǎn)![]() 恰好在函數(shù)
恰好在函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() ,
,![]() )的圖象上,且四邊形
)的圖象上,且四邊形![]() 為平行四邊形,求此時(shí)
為平行四邊形,求此時(shí)![]() 、
、![]() 的長(zhǎng)度.
的長(zhǎng)度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】《九章算術(shù)》是中國(guó)傳統(tǒng)數(shù)學(xué)最重要的著作,在“勾股”章中有這樣一個(gè)問(wèn)題:“今有邑方二百步,各中開門,出東門十五步有木,問(wèn):出南門幾步而見木?”
用今天的話說(shuō),大意是:如圖,![]() 是一座邊長(zhǎng)為200步(“步”是古代的長(zhǎng)度單位)的正方形小城,東門
是一座邊長(zhǎng)為200步(“步”是古代的長(zhǎng)度單位)的正方形小城,東門![]() 位于
位于![]() 的中點(diǎn),南門
的中點(diǎn),南門![]() 位于
位于![]() 的中點(diǎn),出東門15步的
的中點(diǎn),出東門15步的![]() 處有一樹木,求出南門多少步恰好看到位于
處有一樹木,求出南門多少步恰好看到位于![]() 處的樹木(即點(diǎn)
處的樹木(即點(diǎn)![]() 在直線
在直線![]() 上)?請(qǐng)你計(jì)算
上)?請(qǐng)你計(jì)算![]() 的長(zhǎng)為__________步.
的長(zhǎng)為__________步.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com