
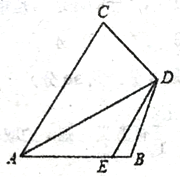
【題目】如圖:四邊形ABDC中,CD=BD,E為AB上一點,連接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,則EB=______________。
【答案】![]()
【解析】
如圖,作DM⊥AC于M,DN⊥AB于N.首先證明Rt△DMC≌Rt△DNB,推出CM=BN,△ADM≌△ADN,推出AM=AB,再證明DE∥AC,推出∠ADE=∠CAD=∠DAB=30°,推出AE=DE,推出∠DEN=60°,在Rt△ADN中,可得DN=ANtan30°=![]() ,在Rt△EDN中,可得DE=DN÷cos30°=
,在Rt△EDN中,可得DE=DN÷cos30°=![]() ,由此即可解決問題.
,由此即可解決問題.
如圖,作DM⊥AC于M,DN⊥AB于N.
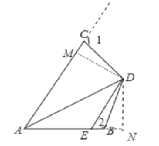
∵∠CAD=∠BAD=30°,DM⊥AC于M,DN⊥AB于N,
∴DN=DM,
在Rt△DMC和Rt△DNB中,
![]() ,
,
∴Rt△DMC≌Rt△DNB,
∴CM=BN,
同理可證△ADM≌△ADN,
∴AM=AB,
∴AC+AB=AM+CM+ANBN=2AM=8,
∴AM=AN=4,
∵∠DCM=∠DBN,
∴∠1=∠2,
∵∠CDE=∠2,
∴∠1=∠CDE,
∴DE∥AC,
∴∠ADE=∠CAD=∠DAB=30°,
∴AE=DE,
∴∠DEN=60°,
在Rt△ADN中,DN=ANtan30°=![]() ,
,
在Rt△EDN中,DE=DN÷cos30°=![]() ,
,
∴AE=![]() ,
,
∴EB=ABAE=3![]() =
=![]() .
.
故答案為![]() .
.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】在正方形網格中建立如圖所示的平面直角坐標系xOy.△ABC的三個頂點都在格點上,點A的坐標是(4,4),請解答下列問題:
(1)將△ABC向下平移5個單位長度,畫出平移后的A1B1C1,并寫出點A的對應點A1的坐標;
(2)畫出△A1B1C1關于y軸對稱的△A2B2C2;
(3)將△ABC繞點C逆時針旋轉90°,畫出旋轉后的△A3B3C.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A.直線外一點到這條直線的垂線段,叫做點到直線的距離;
B.已知線段![]() ,
,![]() 軸,若點
軸,若點![]() 的坐標為(-1,2),則點
的坐標為(-1,2),則點![]() 的坐標為(-1,-2)或(-1,6);
的坐標為(-1,-2)或(-1,6);
C.若![]() 與
與![]() 互為相反數,則
互為相反數,則![]() ;
;
D.已知關于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,則
,則![]() 的取值范圍為
的取值范圍為![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知RT△ABC中,∠C=90°,AC=4,BC=8.動點P從點C出發,以每秒2個單位的速度沿射線CB方向運動,連接AP,設運動時間為ts.
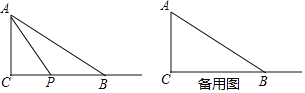
(1)求斜邊AB的長
(2)當t為何值時,△PAB的面積為6
(3)若t<4,請在所給的圖中畫出△PAB中AP邊上的高BQ,問:當t為何值時,BQ長為4?并求出此時點Q到邊BC的距離
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O是△ABC的外心,I是△ABC的內心,連AI并延長交BC和⊙O于D、E兩點.
(1)求證:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸的單位長度為1
![]()
(1)如果點![]() 表示的數互為相反數,那么點
表示的數互為相反數,那么點![]() 表示的數是_______,點
表示的數是_______,點![]() 表示的數是_______;
表示的數是_______;
(2)如果點![]() 表示的數互為相反數,那么四點中,點_______表示的數的絕對值最大,請簡要說明理由;
表示的數互為相反數,那么四點中,點_______表示的數的絕對值最大,請簡要說明理由;
(3)當點![]() 為原點時,若存在一點
為原點時,若存在一點![]() 到點
到點![]() 的距離是點
的距離是點![]() 到點
到點![]() 的距離的2倍,則點
的距離的2倍,則點![]() 所表示的數是_______.
所表示的數是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
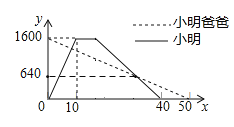
【題目】小明從家出發到公園晨練,在公園鍛煉一段時間后按原路返回,同時小明爸爸從公園按小明的路線返回家中.如圖是兩人離家的距離![]() (米)與小明出發的時間
(米)與小明出發的時間![]() (分)之間的關系,則小明出發______分鐘后與爸爸相遇.
(分)之間的關系,則小明出發______分鐘后與爸爸相遇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,F為CD上一點,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度數為整數,則∠C的度數為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com