
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑的⊙
為直徑的⊙![]() 與邊
與邊![]() 分別交于
分別交于![]() 兩點,過點
兩點,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() .
.

⑴求證:![]() 是⊙
是⊙![]() 的切線;
的切線;
⑵若![]() ,求
,求![]() 的長
的長
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:(1)證明:如圖,連接OD,作OG⊥AC于點G,推出∠ODB=∠C;然后根據(jù)DF⊥AC,∠DFC=90°,推出∠ODF=∠DFC=90°,即可推出DF是⊙O的切線.(2)首先判斷出:AG=![]() AE=2,然后判斷出四邊形OGFD為矩形,即可求出DF的值.
AE=2,然后判斷出四邊形OGFD為矩形,即可求出DF的值.
試題解析:
(1)證明:如圖,連接OD,作OG⊥AC于點G,

∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∵DF⊥AC,
∴∠DFC=90°,
∴∠ODF=∠DFC=90°,
∴DF是⊙O的切線.
(2)解:AG=![]() AE=2,
AE=2,
∵cosA=![]() ,
,
∴OA=![]() =
=![]() =5,
=5,
∴OG=![]() ,
,
∵∠ODF=∠DFG=∠OGF=90°,
∴四邊形OGFD為矩形,
∴DF=OG=![]() .
.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象相交于
的圖象相交于![]() 和
和![]() 兩點.
兩點.
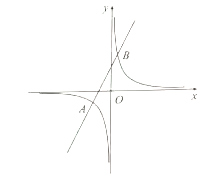
(1)求![]() 的值;
的值;
(2)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,與反比例函數(shù)
,與反比例函數(shù)![]() 的圖象相交于點
的圖象相交于點![]() .若
.若![]() ,求
,求![]() 的值;
的值;
(3)直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,斜邊
,斜邊![]() 的兩個端點分別在相互垂直的射線
的兩個端點分別在相互垂直的射線![]() 上滑動,下列結論:
上滑動,下列結論:
①若![]() 兩點關于
兩點關于![]() 對稱,則
對稱,則![]() ;
;
②![]() 兩點距離的最大值為
兩點距離的最大值為![]() ;
;
③若![]() 平分
平分![]() ,則
,則![]() ;
;
④斜邊![]() 的中點
的中點![]() 運動路徑的長為
運動路徑的長為![]() .
.
其中正確的是 .

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】定義:
數(shù)學活動課上,李老師給出如下定義:如果一個三角形有一邊上的中線等于這條邊的一半,那么稱三角形為“智慧三角形”.

理解:
⑴如圖![]() ,已知
,已知![]() 是⊙
是⊙![]() 上兩點,請在圓上找出滿足條件的點
上兩點,請在圓上找出滿足條件的點![]() ,使
,使![]() 為“智慧三角形”(畫出點
為“智慧三角形”(畫出點![]() 的位置,保留作圖痕跡);
的位置,保留作圖痕跡);
⑵如圖![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 上一點,且
上一點,且![]() ,試判斷
,試判斷![]() 是否為“智慧三角形”,并說明理由;
是否為“智慧三角形”,并說明理由;
運用:
⑶如圖![]() ,在平面直角坐標系
,在平面直角坐標系![]() 中,⊙
中,⊙![]() 的半徑為
的半徑為![]() ,點
,點![]() 是直線
是直線![]() 上的一點,若在⊙
上的一點,若在⊙![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 為“智慧三角形”,當其面積取得最小值時,直接寫出此時點
為“智慧三角形”,當其面積取得最小值時,直接寫出此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】菱形ABCD的對角線AC,BD相交于點O,E,F(xiàn)分別是AD,CD邊上的中點,連接EF.若EF= ![]() ,BD=2,則菱形ABCD的面積為 .
,BD=2,則菱形ABCD的面積為 . 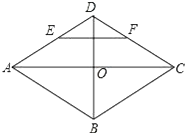
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列關于全等三角形的說法不正確的是
A. 全等三角形的大小相等 B. 兩個等邊三角形一定是全等三角形
C. 全等三角形的形狀相同 D. 全等三角形的對應邊相等
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com