
【題目】已知拋物線y=(m﹣1)x2+(m﹣2)x﹣1與x軸相交于A、B兩點,且AB=2,求m的值.
【答案】解:設(shè)點A(α,0),點B的坐標(biāo)為(β,0)
則一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0的兩根為α、β,
∴α+β=﹣ ![]() ,αβ=﹣
,αβ=﹣ ![]() ,
,
∴|α﹣β|= ![]() =2,
=2,
∴(α+β)2﹣4αβ=4,
即(﹣ ![]() )2+
)2+ ![]() =4,
=4,
解得m=2或m= ![]()
【解析】抓住已知點A、B是拋物線與x軸的兩交點坐標(biāo),設(shè)點A(α,0),點B的坐標(biāo)為(β,0),可知一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0的兩根為α、β,再利用根與系數(shù)的關(guān)系求出α+β和αβ的值,再根據(jù)AB=|α﹣β|=2,列出關(guān)于m的方程求解即可。
【考點精析】利用根與系數(shù)的關(guān)系和二次函數(shù)圖象以及系數(shù)a、b、c的關(guān)系對題目進(jìn)行判斷即可得到答案,需要熟知一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數(shù)a、b、c而定;兩根之和等于方程的一次項系數(shù)除以二次項系數(shù)所得的商的相反數(shù);兩根之積等于常數(shù)項除以二次項系數(shù)所得的商;二次函數(shù)y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關(guān):對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標(biāo):(0,c).


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)課上,王老師布置如下任務(wù):如圖,△ABC中,BC>AB>AC,在BC邊上取一點P,使∠APC=2∠ABC.

小路的作法如下:
① 作AB邊的垂直平分線,交BC于點P,交AB于點Q;
② 連結(jié)AP.
請你根據(jù)小路同學(xué)的作圖方法,利用直尺和圓規(guī)完成作圖(保留作圖痕跡);并完成以下推理,注明其中蘊(yùn)含的數(shù)學(xué)依據(jù):
∵ PQ是AB的垂直平分線
∴ AP= , (依據(jù): );
∴ ∠ABC= , (依據(jù): ).
∴ ∠APC=2∠ABC.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某書店老板去圖書批發(fā)市場購買某種圖書.第一次用1200元購書若干本,并按該書定價7元出售,很快售完.由于該書暢銷,第二次購書時,每本書的批發(fā)價已比第一次提高了20%,他用1500元所購該書數(shù)量比第一次多10本.當(dāng)按定價7元售出150本時,出現(xiàn)滯銷,便以定價的5折售完剩余的書.
(1)每本書第一次的批發(fā)價是多少錢?
(2)試問該老板這兩次售書總體上是賠錢了,還是賺錢了(不考慮其它因素)?若賠錢,賠多少?若賺錢,賺多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將□ABCD如圖放置,若點B的坐標(biāo)是(-3,4),點C的坐標(biāo)是(-1,0),點D的坐標(biāo)是(5,3),則點A的坐標(biāo)是______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在ABCD中,AE⊥BD,CF⊥BD,E,F分別為垂足.
(1)求證:四邊形AECF是平行四邊形;
(2)如果AE=3,EF=4,求AF、EC所在直線的距離.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,∠C=90°,
(1)若a=4,b=3,則c=_______;
(2)若a=24,c=30,則b=_______;
(3)若BC=11,AB=61,則AC=_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,在△ABC中,∠A=90°,AB=AC,點D為BC的中點.
(1)如圖①,若點E、F分別為AB、AC上的點,且DE⊥DF,求證:BE=AF;
(2)若點E、F分別為AB、CA延長線上的點,且DE⊥DF,那么BE=AF嗎?請利用圖②說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)中,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,將線段
,將線段![]() 向右平移
向右平移![]() 個單位長度得到線段
個單位長度得到線段![]() (點
(點![]() 和點
和點![]() 分別是點
分別是點![]() 和點
和點![]() 的對應(yīng)點),連接
的對應(yīng)點),連接![]() 、
、![]() ,點
,點![]() 是線段
是線段![]() 的中點.
的中點.

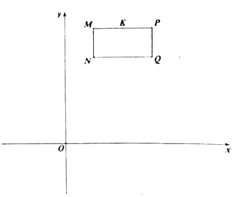
備用圖
(1)求點![]() 的坐標(biāo);
的坐標(biāo);
(2)若長方形![]() 以每秒
以每秒![]() 個單位長度的速度向正下方運(yùn)動,(點
個單位長度的速度向正下方運(yùn)動,(點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分別是點
分別是點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的對應(yīng)點),當(dāng)
的對應(yīng)點),當(dāng)![]() 與
與![]() 軸重合時停止運(yùn)動,連接
軸重合時停止運(yùn)動,連接![]() 、
、![]() ,設(shè)運(yùn)動時間為
,設(shè)運(yùn)動時間為![]() 妙,請用含
妙,請用含![]() 的式子表示三角形
的式子表示三角形![]() 的面積
的面積![]() (不要求寫出
(不要求寫出![]() 的取值范圍);
的取值范圍);
(3)在(2)的條件下,連接![]() 、
、![]() ,問是否存在某一時刻
,問是否存在某一時刻![]() ,使三角形
,使三角形![]() 的面積等于三角形
的面積等于三角形![]() 的面積?若存在,請求出
的面積?若存在,請求出![]() 值;若不存在,請說明理由.
值;若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com