

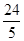 ;(4)4.
;(4)4. AD,根據題意,列出關于t的方程,通過解方程來求t的值;③當∠DEF=90°時,此時∠ADE=90°-∠A=30°,此時AD=
AD,根據題意,列出關于t的方程,通過解方程來求t的值;③當∠DEF=90°時,此時∠ADE=90°-∠A=30°,此時AD= AE,根據題意,列出關于t的方程,通過解方程來求t的值.
AE,根據題意,列出關于t的方程,通過解方程來求t的值. CD=
CD= ×2t=t.
×2t=t. AD,∴t=
AD,∴t= (12?2t).∴t=3.
(12?2t).∴t=3. AE.∴12?2t=
AE.∴12?2t= t.∴t=
t.∴t=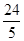 .
.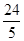 秒時,△DEF為直角三角形.
秒時,△DEF為直角三角形.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:初中數學 來源:不詳 題型:解答題
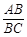 =k.
=k.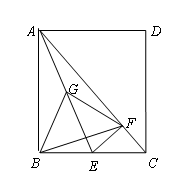
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
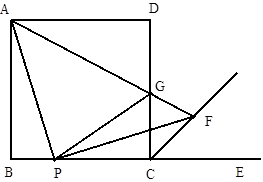
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
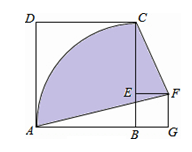
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.7 | B.8 | C.9 | D.10 |

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
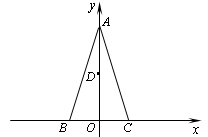
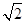 ),C(1,0), D為射線AO上一點,一動點P從A出發,運動路徑為A→D→C,點P在AD上的運動速度是在CD上的3倍,要使整個運動時間最少,則點D的坐標應為( )
),C(1,0), D為射線AO上一點,一動點P從A出發,運動路徑為A→D→C,點P在AD上的運動速度是在CD上的3倍,要使整個運動時間最少,則點D的坐標應為( )A.(0,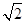 ) ) | B.(0,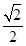 ) ) | C.(0, ) ) | D.(0,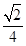 ) ) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com