
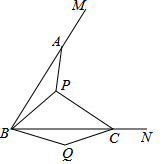
 如圖,已知∠MBN=60°,在BM,BN上分別截取BA=BC,P是∠MBN內(nèi)的一點(diǎn),連接PA,PB,PC,以BP為邊作∠PBQ=60°,且BQ=BP,連接CQ.
如圖,已知∠MBN=60°,在BM,BN上分別截取BA=BC,P是∠MBN內(nèi)的一點(diǎn),連接PA,PB,PC,以BP為邊作∠PBQ=60°,且BQ=BP,連接CQ.分析 (1)易證△ABP≌△CBQ,可得AP=CQ;
(2)根據(jù)PA=CQ,PB=BQ,即可判定△PQC為直角三角形.
解答 (1)解:AP=CQ;理由如下:
連接PQ,如圖所示:
∵∠PBQ=60°,且BQ=BP,
∴△BPQ為等邊三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABP=∠CBQ}&{\;}\\{BP=BQ}&{\;}\end{array}\right.$,
∴△ABP≌△CBQ(SAS),
∴AP=CQ,
(2)證明:設(shè)PA=3a,PB=4a,PC=5a,
在△PBQ中,∵PB=BQ=4a,且∠PBQ=60°,
∴△PBQ為等邊三角形,
∴PQ=4a,
在△PQC中,∵PQ2+QC2=16a2+9a2=25a2=PC2,
∴△PQC為直角三角形,即∠PQC=90°.
點(diǎn)評(píng) 本題考查了全等三角形的判定,考查了全等三角形對(duì)應(yīng)邊相等的性質(zhì),考查了勾股定理逆定理的運(yùn)用,本題中求證△ABP≌△CBQ是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
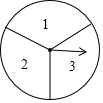 如圖,一個(gè)轉(zhuǎn)盤被分成3等分,每一份上各寫有一個(gè)數(shù)字,隨機(jī)轉(zhuǎn)動(dòng)轉(zhuǎn)盤2次,第一次轉(zhuǎn)到的數(shù)字?jǐn)?shù)字為十位數(shù)字,第二次轉(zhuǎn)到的數(shù)字為個(gè)位數(shù)字,2次轉(zhuǎn)動(dòng)后組成一個(gè)兩位數(shù)(若指針停在等分線上則重新轉(zhuǎn)一次)
如圖,一個(gè)轉(zhuǎn)盤被分成3等分,每一份上各寫有一個(gè)數(shù)字,隨機(jī)轉(zhuǎn)動(dòng)轉(zhuǎn)盤2次,第一次轉(zhuǎn)到的數(shù)字?jǐn)?shù)字為十位數(shù)字,第二次轉(zhuǎn)到的數(shù)字為個(gè)位數(shù)字,2次轉(zhuǎn)動(dòng)后組成一個(gè)兩位數(shù)(若指針停在等分線上則重新轉(zhuǎn)一次)查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com