
【題目】如圖,正方形![]() 邊長為2,
邊長為2,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上兩動點,且滿足
上兩動點,且滿足![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
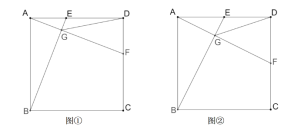
(1)如圖1,判斷線段![]() 、
、![]() 的位置關(guān)系,并說明理由;
的位置關(guān)系,并說明理由;
(2)在(1)的條件下,連接![]() ,直接寫出
,直接寫出![]() 的最小值為 ;
的最小值為 ;
(3)如圖2,點![]() 為
為![]() 的中點,連接
的中點,連接![]() .
.
①求證:![]() 平分
平分![]() ;
;
②求線段![]() 的長度.
的長度.
【答案】(1)![]() ;理由見解析;(2)
;理由見解析;(2)![]() ;(3)①見解析;②
;(3)①見解析;②![]() .
.
【解析】
(1)證明![]() ,即可解答.
,即可解答.
(2)取AB的中點0,連接OG、OD,則OG=![]() AB=1,在Rt△AOD中,根據(jù)勾股定理計算出OD的值;根據(jù)三角形的三邊關(guān)系,可得OG+DG>OD,于是當O、D、G三點共線時,DG的長度最小為OD-OG,據(jù)此解答.
AB=1,在Rt△AOD中,根據(jù)勾股定理計算出OD的值;根據(jù)三角形的三邊關(guān)系,可得OG+DG>OD,于是當O、D、G三點共線時,DG的長度最小為OD-OG,據(jù)此解答.
(3)①過點![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,可得四邊形
,可得四邊形![]() 為矩形,再證得
為矩形,再證得![]() ,所以
,所以![]() ,又因為
,又因為![]() ,
, ![]() ,可得
,可得![]() 平分
平分![]() ;
;
②在![]() 中,根據(jù)
中,根據(jù)![]() ,可求得DN,在
,可求得DN,在![]() 中,
中,![]() ,
,![]() ,即可求得DG.
,即可求得DG.
(1)![]() ;理由:
;理由:
∵四邊形![]() 為正方形.
為正方形.
∴![]() ,
,![]() ,
,
∵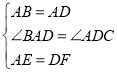 ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)取AB的中點O,連接OG、OD,如圖所示:
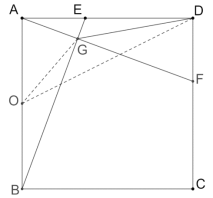
則OG=![]() AB=1
AB=1
在Rt△AOD中,OD=![]()
根據(jù)三角形的三邊關(guān)系,OG+DG>OD,當O、D、G三點共線時,DG的長度最小,最小值=OD-OG=![]()
故答案為:![]()
(3)①過點![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() .
.
∴四邊形![]() 為矩形,
為矩形,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 平分
平分![]() ;
;
②在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.

故答案為:![]()


科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,函數(shù)
中,函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,直線
,直線![]() 與x軸交于點
與x軸交于點![]() .
.
(1)求![]() 的值;
的值;
(2)過第二象限的點![]() 作平行于x軸的直線,交直線
作平行于x軸的直線,交直線![]() 于點C,交函數(shù)
于點C,交函數(shù)![]() 的圖象于點D.
的圖象于點D.
①當![]() 時,判斷線段PD與PC的數(shù)量關(guān)系,并說明理由;
時,判斷線段PD與PC的數(shù)量關(guān)系,并說明理由;
②若![]() ,結(jié)合函數(shù)的圖象,直接寫出n的取值范圍.
,結(jié)合函數(shù)的圖象,直接寫出n的取值范圍.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在全國初中數(shù)學聯(lián)賽中,將參賽兩個班學生的成績(得分均為整數(shù))進行整理后分成五組,繪制出如下的頻率分布直方圖(如圖所示),已知圖中從左到右的第一、第三、第四、第五小組的頻率分別是0.25、0.15、0.10、0.10,第二組的頻數(shù)是40.
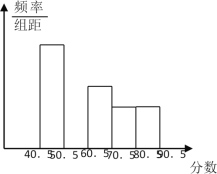
(1)第二小組的頻率是_____,并補全這個頻率分布直方圖;
(2)這兩個班參賽的學生人數(shù)是_________;
(3)這兩個班參賽學生的成績的中位數(shù)落在第______組內(nèi).(不必說明理由)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】2016年4月23日是我國第一個“全民閱讀日”某校開展了“建設(shè)書香校園,捐贈有益圖書”活動.我們在參加活動的所有班級中,隨機抽取了一個班,已知這個班是八年級5班,全班共50名學生.現(xiàn)將該班捐贈圖書情況的統(tǒng)計結(jié)果,繪制成如下兩幅不完整的統(tǒng)計圖.
請你根據(jù)以上信息,解答下列問題:
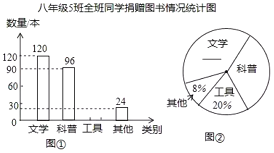
(1)補全上面的條形統(tǒng)計圖和扇形統(tǒng)計圖;
(2)求八年級5班平均每人捐贈了多少本書?
(3)若該校八年級共有800名學生,請你估算這個年級學生共可捐贈多少本書?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)![]() (
(![]() 為常數(shù)),當自變量
為常數(shù)),當自變量![]() 的值滿足
的值滿足![]() 時,其對應(yīng)的函數(shù)值
時,其對應(yīng)的函數(shù)值![]() 的最大值為
的最大值為![]() ,則
,則![]() 的值為 ( )
的值為 ( )
A.2或4B.0或-4C.2或-4D.0或4
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】六![]() 一前夕,某幼兒園園長到廠家選購A、B兩種品牌的兒童服裝,每套A品牌服裝進價比B品牌服裝每套進價多25元,用2000元購進A種服裝數(shù)量是用750元購進B種服裝數(shù)量的2倍.
一前夕,某幼兒園園長到廠家選購A、B兩種品牌的兒童服裝,每套A品牌服裝進價比B品牌服裝每套進價多25元,用2000元購進A種服裝數(shù)量是用750元購進B種服裝數(shù)量的2倍.
![]() 求A、B兩種品牌服裝每套進價分別為多少元?
求A、B兩種品牌服裝每套進價分別為多少元?
![]() 該服裝A品牌每套售價為130元,B品牌每套售價為95元,服裝店老板決定,購進B品牌服裝的數(shù)量比購進A品牌服裝的數(shù)量的2倍還多4套,兩種服裝全部售出后,可使總的獲利超過1200元,則最少購進A品牌的服裝多少套?
該服裝A品牌每套售價為130元,B品牌每套售價為95元,服裝店老板決定,購進B品牌服裝的數(shù)量比購進A品牌服裝的數(shù)量的2倍還多4套,兩種服裝全部售出后,可使總的獲利超過1200元,則最少購進A品牌的服裝多少套?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】揚州某風景區(qū)門票價格如圖所示,有甲、乙兩個旅行團隊,計劃在端午節(jié)期間到該景點游玩,兩團隊游客人數(shù)之和為100人,若乙團隊人數(shù)不超過40人,甲團隊人數(shù)不超過80人,設(shè)甲團隊人數(shù)為![]() 人,如果甲、乙兩團隊分別購買門票,兩團隊門票款之和為
人,如果甲、乙兩團隊分別購買門票,兩團隊門票款之和為![]() 元.
元.
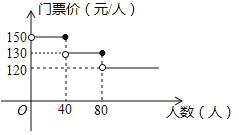
(1)直接寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并寫出自變量
的函數(shù)關(guān)系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)計算甲、乙兩團隊聯(lián)合購票比分別購票最多可節(jié)約多少錢?
(3)該景區(qū)每年11月、12月為淡季,景區(qū)決定在這兩個月實行門票打五折的優(yōu)惠(打折期間不售團體票),以吸引大量游客,提高景區(qū)收入;景區(qū)經(jīng)過調(diào)研發(fā)現(xiàn),隨著接待游客數(shù)的增加,景區(qū)的運營成本也隨之增加,景區(qū)運營成本![]() (萬元)與兩個月游客總?cè)藬?shù)
(萬元)與兩個月游客總?cè)藬?shù)![]() (萬人)之間滿足函數(shù)關(guān)系式:
(萬人)之間滿足函數(shù)關(guān)系式:![]() ;兩個月游客總?cè)藬?shù)
;兩個月游客總?cè)藬?shù)![]() (萬人)滿足:
(萬人)滿足:![]() ,且淡季每天游客數(shù)基本相同;為了獲得最大利潤,景區(qū)決定通過網(wǎng)絡(luò)預(yù)約購票的方式控制淡季每天游客數(shù),請問景區(qū)的決定是否正確?并說明理由.(利潤
,且淡季每天游客數(shù)基本相同;為了獲得最大利潤,景區(qū)決定通過網(wǎng)絡(luò)預(yù)約購票的方式控制淡季每天游客數(shù),請問景區(qū)的決定是否正確?并說明理由.(利潤![]() 門票收入
門票收入![]() 景區(qū)運營成本)
景區(qū)運營成本)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下面材料:
小明遇到這樣一個問題:
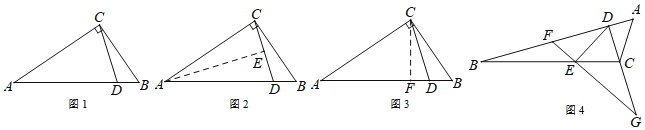
如圖1,△ABC中,∠ACB=90°,點D在AB上,且∠BAC=2∠DCB,求證:AC=AD.
小明發(fā)現(xiàn),除了直接用角度計算的方法外,還可以用下面兩種方法:
方法1:如圖2,作AE平分∠CAB,與CD相交于點E.
方法2:如圖3,作∠DCF=∠DCB,與AB相交于點F.
(1)根據(jù)閱讀材料,任選一種方法,證明AC=AD.
用學過的知識或參考小明的方法,解決下面的問題:
(2)如圖4,△ABC中,點D在AB上,點E在BC上,且∠BDE=2∠ABC,點F在BD上,且∠AFE=∠BAC,延長DC、FE,相交于點G,且∠DGF=∠BDE.
①在圖中找出與∠DEF相等的角,并加以證明;
②若AB=kDF,猜想線段DE與DB的數(shù)量關(guān)系,并證明你的猜想.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
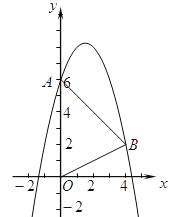
【題目】如圖,拋物線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點.
兩點.
(1)求拋物線的解析式;
(2)將拋物線向下平移![]() 個單位,使平移后得到的拋物線頂點落在
個單位,使平移后得到的拋物線頂點落在![]() 的內(nèi)部(不包括
的內(nèi)部(不包括![]() 的邊界),求
的邊界),求![]() 的取值范圍.
的取值范圍.
(3)若![]() 是拋物線上一動點,是否存在點
是拋物線上一動點,是否存在點![]() ,使
,使![]() 的面積是
的面積是![]() ?若存在,直接寫出P點坐標;若不存在,請說明理由.
?若存在,直接寫出P點坐標;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com