
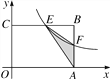
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y=![]() (x>0)的圖象與BC邊交于點E.
(x>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?
【答案】(1)y=![]() (x>0)(2)當k=3時,S△EFA有最大值,最大值為
(x>0)(2)當k=3時,S△EFA有最大值,最大值為![]() .
.
【解析】試題分析:(1)、首先得出點B的坐標,然后根據中點得出點F的坐標,最后利用待定系數法求出函數解析式;(2)、首先得出點E和點F的坐標,然后根據三角形的面積計算法則得出關于k的二次函數,然后根據函數的增減性得出最大值.
試題解析:(1)∵在矩形OABC中,OA=3,OC=2, ∴B(3,2),∵F為AB的中點,
∴F(3,1), ∵點F在反比例函數y=![]() (k>0)的圖象上, ∴k=3,
(k>0)的圖象上, ∴k=3,
∴該函數的解析式為y=![]() (x>0);
(x>0);
(2)由題意知E,F兩點坐標分別為E(![]() ,2),F(3,
,2),F(3,![]() ),
),
∴S△EFA=![]() AFBE=
AFBE=![]() ×
×![]() k(3﹣
k(3﹣![]() k)=
k)=![]() k﹣
k﹣![]() k2=﹣
k2=﹣![]() (k2﹣6k+9﹣9)=﹣
(k2﹣6k+9﹣9)=﹣![]() (k﹣3)2+
(k﹣3)2+![]()
當k=3時,S有最大值.
S最大值=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
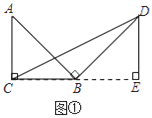
【題目】問題原型:如圖①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.過點D作△BCD的BC邊上的高DE, 易證△ABC≌△BDE,從而得到△BCD的面積為![]() .
.
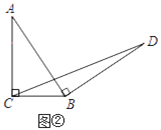
初步探究:如圖②,在Rt△ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.用含a的代數式表示△BCD的面積,并說明理由.
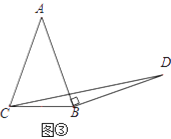
簡單應用:如圖③,在等腰三角形ABC中,AB=AC,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.直接寫出△BCD的面積.(用含a的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某專賣店專營某品牌的襯衫,店主對上一周中不同尺碼的襯衫銷售情況統計如下:
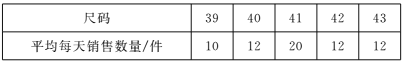
該店主決定本周進貨時,增加一些41碼的襯衫,影響該店主決策的統計量是( )
A.平均數 B.方差 C.眾數 D.中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-3,2),B(0,4),C(0,2).

(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△![]() C;平移△ABC,若A的對應點
C;平移△ABC,若A的對應點![]() 的坐標為(0,4),畫出平移后對應的△
的坐標為(0,4),畫出平移后對應的△![]() ;
;
(2)若將△![]() C繞某一點旋轉可以得到△
C繞某一點旋轉可以得到△![]() ,請直接寫出旋轉中心的坐標;
,請直接寫出旋轉中心的坐標;
(3)在![]() 軸上有一點P,使得PA+PB的值最小,請直接寫出點P的坐標.
軸上有一點P,使得PA+PB的值最小,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料,回答問題:
解方程x4-5x2+4=0,這是一個一元四次方程,根據該方程的特點,它的解法通常是:
設x2=y,那么x4=y2,于是原方程可變為y2-5y+4=0 ①,解得y1=1,y2=4.
當y=1時,x2=1,∴x=±1;當y=4時,x2=4,∴x=±2;
∴原方程有四個根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的過程中,利用 法(把未知數x換為 y)達到降次的目的.
(2)解方程:(x2+3x)2+5(x2+3x)-6=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
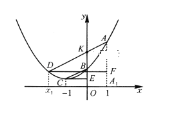
【題目】如圖,已知點A(1,yA),B(0,yB),C(-1,yC),D(x1,yD)(x1≠1)在拋物線![]() 上,且AD//BC,AA1
上,且AD//BC,AA1![]() 軸于A1,DF⊥AAl于F,CE⊥
軸于A1,DF⊥AAl于F,CE⊥![]() 軸于E.
軸于E.
(1)求證:△ADF∽△BCE;
(2)當![]() ,
,![]() ,
,![]() 時,求
時,求![]() 的值;
的值;
(3)![]() 的值會隨a,b,c的值改變而改變嗎?若會,請求出
的值會隨a,b,c的值改變而改變嗎?若會,請求出![]() 與a,b,c的關系式;若不會,請說明理由.
與a,b,c的關系式;若不會,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖所示,對稱軸是直線x=-1,有以下結論:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正確的結論的個數是( )
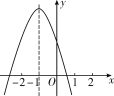
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于頻率與概率有下列幾種說法:①“明天下雨的概率是90%”表示明天下雨的可能性很大;②“拋一枚硬幣正面朝上的概率為![]() ”表示每拋兩次就有一次正面朝上;③“某彩票中獎的概率是1%”表示買10張該種彩票不可能中獎;④“拋一枚硬幣正面朝上的概率為
”表示每拋兩次就有一次正面朝上;③“某彩票中獎的概率是1%”表示買10張該種彩票不可能中獎;④“拋一枚硬幣正面朝上的概率為![]() ”表示隨著拋擲次數的增加,“拋出正面朝上”這一事件發生的頻率穩定在
”表示隨著拋擲次數的增加,“拋出正面朝上”這一事件發生的頻率穩定在![]() 附近,正確的說法是( )
附近,正確的說法是( )
A. ②④B. ②③C. ①④D. ①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發商場銷售一種高檔水果,如果每千克盈利10元,每天可售出500千克,經市場調查發現,在進貨價不變的情況下.若每千克漲價1元,日銷售量將減少20千克.
(1)現該商場要保證每天盈利6000元,同時又要使顧客得到實惠,那么每千克應漲價多少元?
(2)每千克水果漲價多少元時,商場每天獲得的利潤最大?獲得的最大利潤是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com