
【題目】如圖,曲線![]() 是拋物線的一部分,與
是拋物線的一部分,與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且表達式
,且表達式![]() ,曲線
,曲線![]() 與曲線
與曲線![]() 關于直線
關于直線![]() 對稱.
對稱.
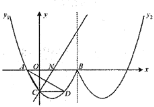
(1)求![]() 三點的坐標和曲線
三點的坐標和曲線![]() 的表達式;
的表達式;
(2)過點![]() 作
作![]() 軸交曲線
軸交曲線![]() 于點
于點![]() ,連結
,連結![]() ,在曲線
,在曲線![]() .上有一點
.上有一點![]() ,使得四邊形
,使得四邊形![]() 為箏形(如果一個四邊形的一條對角線被另一條對角線垂直平分,這樣的四邊形為箏形),請求出點
為箏形(如果一個四邊形的一條對角線被另一條對角線垂直平分,這樣的四邊形為箏形),請求出點![]() 的橫坐標.
的橫坐標.
【答案】(1)A(-1, 0)、B(3, 0)、C(0, ![]() );
);![]()
![]() (x≥3);(2)
(x≥3);(2)![]() .
.
【解析】
(1)當![]() 時,解得x=-1或3;當x=0時,
時,解得x=-1或3;當x=0時,![]() ,從而求出點A、B、C的坐標,利用對稱性求出點A和點B關于直線x=3的對稱點,利用待定系數(shù)法即可求出
,從而求出點A、B、C的坐標,利用對稱性求出點A和點B關于直線x=3的對稱點,利用待定系數(shù)法即可求出![]() 的表達式;
的表達式;
(2)利用對稱性求出點D的坐標,根據(jù)平面直角坐標系中兩點之間的距離公式即可求出AC=DC=2,從而得出點C在AD的垂直平分線上,過點A、M分別作x軸的垂線,與直線CD分別交于點G、H,那么∠ADG=∠CMH,根據(jù)銳角三角函數(shù)求出∠ADC,設M![]() ,列出方程即可求出結論.
,列出方程即可求出結論.
解:(1)由![]()
![]() ,
,
當![]() 時,解得x=-1或3;當x=0時,
時,解得x=-1或3;當x=0時,![]() ;
;
∴A(-1, 0)、B(3, 0)、C(0, ![]() ).
).
∵A(-1, 0)、B(3, 0) 關于直線x=3的對稱點為A′(7, 0)、B(3, 0),
∴拋物線y2的表達式為:![]()
![]() (x≥3).
(x≥3).
(2)由CD//x軸,可知C、D關于拋物線y1的對稱軸x=1對稱,
所以D(2,![]() ).
).
由A(-1, 0)、C(0,![]() )、D(2,
)、D(2,![]() ),
),
∴AC=![]() ,CD=2
,CD=2
∴AC=DC=2.
∴點C在AD的垂直平分線上.
如果四邊形ACDM的對角線互相垂直平分,那么四邊形ACDM是菱形,此時點M在x軸上,不在拋物線y2上.因此只存在MC垂直平分AD的情況.
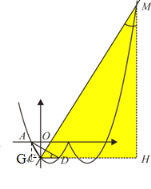
如上圖,過點A、M分別作x軸的垂線,與直線CD分別交于點G、H,那么∠ADG=∠CMH.
由于tan∠ADG=![]() =
=![]() ,所以∠ADC=30°.因此
,所以∠ADC=30°.因此![]() .
.
設M![]() ,那么
,那么![]() .
.
整理,得x2-13x+24=0.解得![]() .
.
所以點M的橫坐標為![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】列方程或方程組解應用題:
北京市實施交通管理新措施以來,全市公共交通客運量顯著增加.據(jù)統(tǒng)計,2008年10月11日到2009年2月28日期間,地面公交日均客運量與軌道交通日均客運量總和為1696萬人次,地面公交日均客運量比軌道交通日均客運量的4倍少69萬人次.在此期間,地面公交和軌道交通日均客運量各為多少萬人次?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 為
為![]() 上一點,
上一點,![]() 和過點
和過點![]() 的切線互相垂直,垂足為
的切線互相垂直,垂足為![]() ,
,![]() 交
交![]() 于點
于點![]() ,直線
,直線![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/STEM/6108b9d591da4e268d6d47ef4c154d16.png]
(1)求證:![]() 平分
平分![]() ;
;
(2)探究線段![]() ,
,![]() 之間的數(shù)量關系,并說明理由;
之間的數(shù)量關系,并說明理由;
(3)若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
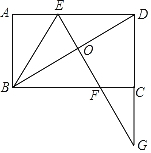
【題目】如圖,已知矩形ABCD,對角線BD的垂直平分線分別交AD,BC和BD于點E,F,O.EF,DC的延長線交于點G,且OD=CG,連接BE.
(1)求證:△DOE≌△GCF;
(2)求證:BE平分∠ABD.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】隨著社會的發(fā)展,物質(zhì)生活極大豐富,青少年的營養(yǎng)過剩,身體越來越胖,某校為了了解八年級學生的體重情況,隨機抽取了八年級部分學生進行調(diào)查,將抽取學生的體重情況繪制成如下不完整的統(tǒng)計圖表,如圖表所示,請根據(jù)圖表信息回答下列問題:
組別 | 體重(千克} | 人數(shù) |
A |
| 3 |
B |
| 12 |
C |
| a |
D |
| 10 |
E |
| 8 |
F |
| 2 |
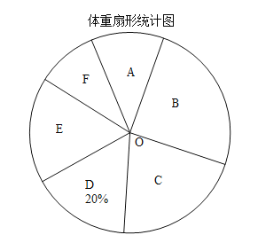
(1)求得![]() __________(直接寫出結果); 在扇形統(tǒng)計圖中,D組所在扇形的圓心角的度數(shù)等于_________ ;
__________(直接寫出結果); 在扇形統(tǒng)計圖中,D組所在扇形的圓心角的度數(shù)等于_________ ;
(2)調(diào)查的這組數(shù)據(jù)的中位數(shù)落在_________組;
(3)如果體重不低于55千克,屬于偏胖,該校八年級有1200名學生,請估算該年級體重偏胖的學生大約有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在某中學開展的“好書伴我成長”讀書活動中,為了解八年級320名學生讀書情況,隨機調(diào)查了八年級部分學生讀書的冊數(shù). 根據(jù)調(diào)查結果,繪制出如下的統(tǒng)計圖①和圖②.請根據(jù)相關信息,解答下列問題:
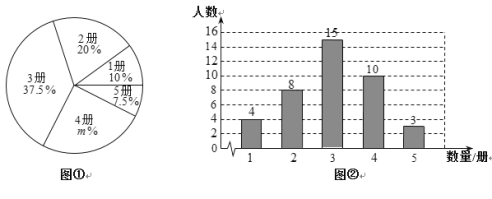
(1)本次接受調(diào)查的學生人數(shù)為 ,圖①中![]() 的值為 ;
的值為 ;
(2)求統(tǒng)計的這組數(shù)據(jù)的平均數(shù)、眾數(shù)和中位數(shù);
(3)根據(jù)統(tǒng)計的樣本數(shù)據(jù),估計該校讀書超過3冊的學生人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】新冠肺炎疫情期間,佩戴口罩是做好個人防護的重要舉措.小明家先后兩次在同一電商平臺以相同的單價免郵購買了![]() 、
、![]() 兩種型號的口罩.第一次購買20個
兩種型號的口罩.第一次購買20個![]() 型口罩,30個
型口罩,30個![]() 型口罩,共花費190元;第二次購買30個
型口罩,共花費190元;第二次購買30個![]() 型口罩,20個
型口罩,20個![]() 型口罩,共花費160元.
型口罩,共花費160元.
(1)求![]() 、
、![]() 兩種型號口罩的單價;
兩種型號口罩的單價;
(2)“五一”期間,該電商平臺舉行促銷活動,小明發(fā)現(xiàn)同樣花費160元購買![]() 型口罩,以活動價購買可以比原價多買8個,求“五一”期間
型口罩,以活動價購買可以比原價多買8個,求“五一”期間![]() 型口罩的活動價.
型口罩的活動價.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,
,![]() ,且與y軸交于點C.
,且與y軸交于點C.
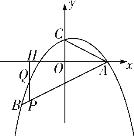
(1)求二次函數(shù)的解析式;
(2)證明:![]() (其中O是原點);
(其中O是原點);
(3)若P是線段![]() 上的一個動點(不與A、B重合),過點P作y軸的平行線,分別交此二次函數(shù)圖象及x軸于Q、H兩點,試問:是否存在這樣的點P,使
上的一個動點(不與A、B重合),過點P作y軸的平行線,分別交此二次函數(shù)圖象及x軸于Q、H兩點,試問:是否存在這樣的點P,使![]() ?若存在,請求出點P的坐標;若不存在,請說明理由.
?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com