
【題目】如圖1,在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() .
.
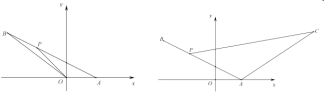
(1)求直線![]() 的函數表達式;
的函數表達式;
(2)點![]() 是線段
是線段![]() 上的一點,當
上的一點,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
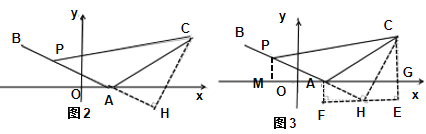
(3)如圖2,在(2)的條件下,將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,點
,點![]() 落在點
落在點![]() 處,連結
處,連結![]() ,求
,求![]() 的面積,并直接寫出點
的面積,并直接寫出點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,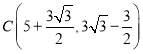 .
.
【解析】
(1)利用待定系數法即可解決問題;
(2)過點![]() 、
、![]() 分別做
分別做![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() ,根據相似三角形的性質得出PM的長,即點P的縱坐標,代入直線解析式,從而求解;
,根據相似三角形的性質得出PM的長,即點P的縱坐標,代入直線解析式,從而求解;
(3)過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,若求
,若求![]() 的面積,求出CH的長即可,根據旋轉120°,得∠CAH=60°,解直角三角形AHC即可得出CH長,從而求解,
的面積,求出CH的長即可,根據旋轉120°,得∠CAH=60°,解直角三角形AHC即可得出CH長,從而求解,
解:(1) )∵A(2,0),![]() ,
,
設直線AB的解析式為y=kx+b,則有![]() ,
,
解得:![]() ,
,
∴直線AB的解析式為![]() .
.
(2)如圖1,過點![]() 、
、![]() 分別做
分別做![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() ,即PM∥BN.
,即PM∥BN.
∵![]() ,
,
∴AP:AB=2:3,
∴![]() =
=![]()
∴![]()
將![]() 代入解析式
代入解析式![]() 可得
可得
![]() ,∴
,∴![]()
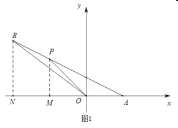
(3)①如圖2,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
∵![]() 中,由勾股定理得:AP=
中,由勾股定理得:AP=![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]() ;
;
②過點H作FE∥x軸,過點C作CE⊥FE于點E,交x軸于點G,過點A作AF⊥FE于點F,
Rt△ACH中, AH=![]() ,
,
∵PM∥AF,AM∥HF,根據直角相等、兩直線平行,同位角相等易證△APM∽△HAF,AP=2![]() ,AM=4,PM=2,
,AM=4,PM=2,
∴![]() ,即
,即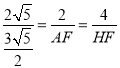 ,
,
解得:AF=![]() ,HF=3,
,HF=3,
∵∠AHF+∠CHE=∠AHF +∠FAH=90°,
∴∠CHE=∠FAH,
∵∠HEC=∠AFH=90°,
∴△HEC∽△AFH,
方法同上得:CE=3![]() ,HE=
,HE=![]() ,
,
由四邊形AFEG是矩形,得AF=GE= ![]() ,AG=FH+HE,
,AG=FH+HE,
∴OG=OA+ FH+HE=2+3+![]() =5+
=5+![]() ,CG=CE-EG=3
,CG=CE-EG=3![]() -
-![]() ,
,
即點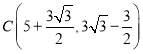 .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,以
中,以![]() 為圓心作⊙
為圓心作⊙![]() ,⊙
,⊙![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() 為⊙
為⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一點,連接
的任意一點,連接![]() 、
、![]() ,過
,過![]() 點分別作
點分別作![]() 于
于![]() ,
,![]() 于
于![]() .設點
.設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() .當
.當![]() 點在⊙
點在⊙![]() 上順時針從點
上順時針從點![]() 運動到點
運動到點![]() 的過程中,下列圖象中能表示
的過程中,下列圖象中能表示![]() 與
與![]() 的函數關系的部分圖象是( )
的函數關系的部分圖象是( )

A.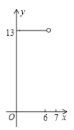 B.
B.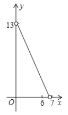 C.
C.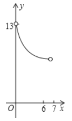 D.
D.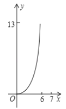
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為響應全民閱讀活動,利用節假日面向社會開放學校圖書館.據統計,第一個月進館128人次,進館人次逐月增加,到第三個月進館達到288人次,若進館人次的月平均增長率相同.
(1)求進館人次的月平均增長率;
(2)因條件限制,學校圖書館每月接納能力不得超過500人次,在進館人次的月平均增長率不變的條件下,校圖書館能否接待第四個月的進館人次,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋子中裝有2個紅球和2個白球,這些球除顏色外其余都相同,先從袋中摸出1個球后不放回,再摸出一個球.
(1)請用樹狀圖或列表法列舉出兩次摸球可能出現的各種結果.
(2)求兩次摸到不同顏色的球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某小區青年對“高鐵”、“掃碼支付”、“網購”和“共享單車”新四大發明的喜愛程度,隨機調查該小區一部分青年(每名青年只能選一個),并將調查結果制成如圖所示統計表與條形統計圖.
青年最喜愛的新四大發明人數統計表
節目 | 人數(名) | 百分比 |
共享單車 | 5 |
|
掃碼支付 | 15 |
|
網購 |
|
|
高鐵 | 10 |
|
青年最喜愛的新四大發明人數條形統計圖
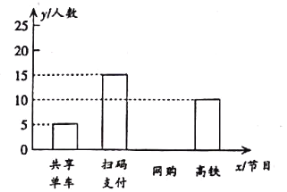
(1)計算![]() 的值
的值![]() ;
;
(2)請補全條形統計圖;
(3)在被調查喜愛“共享單車”青年中,小明一周內使用共享單車的次數分別為:1,3,5,12,![]() ,若整數
,若整數![]() 是這組數據的中位數,直接寫出該組數據的平均數.
是這組數據的中位數,直接寫出該組數據的平均數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某玩具公司生產一種電子玩具,每只玩具的生產成本為18元,試銷過程中發現,每月銷售量y(萬只)與銷售單價x(元)之間的關系可以近似的看作一次函數y=2x+100,設每月銷售這種玩具的利潤為w(萬元).
(1)寫出w與x之間的函數表達式;
(2)當銷售單價為多少元時,公司每月獲得的利潤為440萬元?
(3)如果公司每月的生產成本不超過540萬元,那么當銷售單價為多少元時,公司每月獲得的利潤最大?最大利潤為多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
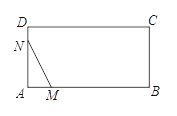
【題目】如圖,在矩形ABCD中,AB=4cm,AD=2cm,動點M自點A出發沿A→B的方向,以每秒1cm的速度運動,同時動點N自點A出發沿A→D→C的方向以每秒2cm的速度運動,當點N到達點C時,兩點同時停止運動,設運動時間為x(秒),△AMN的面積為y(cm2),則下列圖象中能反映y與x之間的函數關系的是( )
A.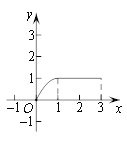 B.
B.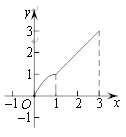 C.
C.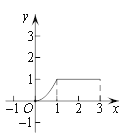 D.
D.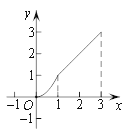
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com