Question

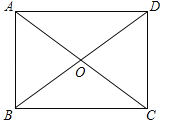
【題目】如圖所示，已知平行四邊形ABCD，對角線AC，BD相交于點O，∠OBC=∠OCB．

（1）求證：平行四邊形ABCD是矩形；

（2）請添加一個條件使矩形ABCD為正方形．

Answer 1

【答案】（1）證明見解析；（2）AB=AD（或AC⊥BD答案不唯一）．

【解析】試題分析：（1）根據平行四邊形對角線互相平分可得OA=OC，OB=OD，根據等角對等邊可得OB=OC，然后求出AC=BD，再根據對角線相等的平行四邊形是矩形證明；

（2）根據正方形的判定方法添加即可．

試題解析：解：（1）∵四邊形ABCD是平行四邊形，∴OA=OC，OB=OD，∵∠OBC=∠OCB，∴OB=OC，∴AC=BD，∴平行四邊形ABCD是矩形；

（2）AB=AD（或AC⊥BD答案不唯一）．

理由：∵四邊形ABCD是矩形，又∵AB=AD，∴四邊形ABCD是正方形．

或：∵四邊形ABCD是矩形，又∵AC⊥BD，∴四邊形ABCD是正方形．