
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊上一動(dòng)點(diǎn),
邊上一動(dòng)點(diǎn),![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,連結(jié)
,連結(jié)![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),則
的中點(diǎn),則![]() 的最小值為________.
的最小值為________.

【答案】![]()
【解析】
根據(jù)矩形的性質(zhì)就可以得出,EF,AP互相平分,且EF=AP,垂線段最短的性質(zhì)就可以得出AP⊥BC時(shí),AP的值最小,即AM的值最小,由勾股定理求出BC,根據(jù)面積關(guān)系建立等式求出其解即可.
:∵四邊形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交點(diǎn)就是M點(diǎn).
∵當(dāng)AP的值最小時(shí),AM的值就最小,
∴當(dāng)AP⊥BC時(shí),AP的值最小,即AM的值最小.
∵![]() AP.BC=
AP.BC=![]() AB.AC,
AB.AC,
∴AP.BC=AB.AC.
在Rt△ABC中,由勾股定理,得
BC=5.
∵AB=3,AC=4,
∴5AP=3×4
∴AP=![]() .
.
∴AM=![]() .
.
故答案為:![]() .
.


 點(diǎn)睛新教材全能解讀系列答案
點(diǎn)睛新教材全能解讀系列答案 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為直徑,
為直徑,![]() 為弦.過
為弦.過![]() 延長(zhǎng)線上一點(diǎn)
延長(zhǎng)線上一點(diǎn)![]() ,作
,作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 是
是![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,
,![]() .
.
(1)判斷![]() 與
與![]() 的位置關(guān)系,并說明理由;
的位置關(guān)系,并說明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】港珠澳大橋是世界最長(zhǎng)的跨海大橋,連接香港大嶼山、澳門半島和廣東省珠海市,其中珠海站到香港站全長(zhǎng)約55千米,2018年10月24日上午9時(shí)正式通車.一輛觀光巴士自珠海站出發(fā),25分鐘后,一輛小汽車從同一地點(diǎn)出發(fā),結(jié)果同時(shí)到達(dá)香港站.已知小汽車的速度是觀光巴士的1.6倍,求觀光巴士的速度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△ABC內(nèi)接于⊙O,BC交直徑AD于點(diǎn)E,過點(diǎn)C作AD的垂線交AB的延長(zhǎng)線于點(diǎn)G,垂足為F.連接OC.
(1)若∠G=48°,求∠ACB的度數(shù);
(2)若AB=AE,求證:∠BAD=∠COF;
(3)在(2)的條件下,連接OB,設(shè)△AOB的面積為S1,△ACF的面積為S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,點(diǎn)E是AD邊的中點(diǎn),BD、CE交于點(diǎn)H,BE、AH交于點(diǎn)G,則下列結(jié)論:①AG⊥BE;②BE:BC=![]() :2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正確的個(gè)數(shù)是
:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正確的個(gè)數(shù)是

A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖(1),已知:在△ABC中,∠BAC=90°,AB=AC,直線m經(jīng)過點(diǎn)A,BD⊥直線m,CE⊥直線m,垂足分別為點(diǎn)D、E.求證:DE=BD+CE.
(2)如圖(2),將(1)中的條件改為:在△ABC中,AB=AC,D、A、E三點(diǎn)都在直線m上,并且有∠BDA=∠AEC=∠BAC=α,其中α為任意銳角或鈍角.請(qǐng)問結(jié)論DE=BD+CE是否成立?如成立,請(qǐng)你給出證明;若不成立,請(qǐng)說明理由.
(3)如圖(3),D、E是D、A、E三點(diǎn)所在直線m上的兩動(dòng)點(diǎn)(D、A、E三點(diǎn)互不重合),點(diǎn)F為∠BAC平分線上的一點(diǎn),且△ABF和△ACF均為等邊三角形,連接BD、CE,若∠BDA=∠AEC=∠BAC,求證:△DEF是等邊三角形.



查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
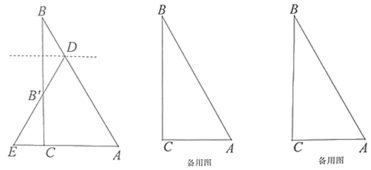
【題目】如圖,已知在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在斜邊
在斜邊![]() 上,將
上,將![]() 沿著過點(diǎn)
沿著過點(diǎn)![]() 的一條直線翻折,使點(diǎn)
的一條直線翻折,使點(diǎn)![]() 落在射線
落在射線![]() 上的點(diǎn)
上的點(diǎn)![]() 處,連接
處,連接![]() 并延長(zhǎng),交射線
并延長(zhǎng),交射線![]() 于
于![]() .
.
(1)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),求BD的長(zhǎng).
重合時(shí),求BD的長(zhǎng).
(2)當(dāng)點(diǎn)![]() 在
在![]() 的延長(zhǎng)線上時(shí),設(shè)
的延長(zhǎng)線上時(shí),設(shè)![]() 為
為![]() ,
,![]() 為
為![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并寫出定義域.
的函數(shù)關(guān)系式,并寫出定義域.
(3)連接![]() ,當(dāng)
,當(dāng)![]() 是直角三角形時(shí),請(qǐng)直接寫出
是直角三角形時(shí),請(qǐng)直接寫出![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(定義)配方法是指將一個(gè)式子或一個(gè)式子的某一部分通過恒等變形化為完全平方式或幾個(gè)完全平
方式的和,這種方法稱之為配方法,例如:可將多項(xiàng)式![]() 通過橫檔變形化為
通過橫檔變形化為![]() 的形式,這個(gè)變形過程中應(yīng)用了配方法.
的形式,這個(gè)變形過程中應(yīng)用了配方法.
(1)(理解)對(duì)于多項(xiàng)式![]() ,當(dāng)x=____________時(shí),它的最小值為______________.
,當(dāng)x=____________時(shí),它的最小值為______________.
(2)(應(yīng)用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三邊,且有
的三邊,且有![]() .
.
①若c為整數(shù),求c的值.
②直接寫出這個(gè)三角形的周長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是一個(gè)被平均分成![]() 等份的轉(zhuǎn)盤,每一個(gè)扇形中都標(biāo)有相應(yīng)的數(shù)字,甲乙兩人分別轉(zhuǎn)動(dòng)轉(zhuǎn)盤,設(shè)甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤后指針?biāo)竻^(qū)域內(nèi)的數(shù)字為
等份的轉(zhuǎn)盤,每一個(gè)扇形中都標(biāo)有相應(yīng)的數(shù)字,甲乙兩人分別轉(zhuǎn)動(dòng)轉(zhuǎn)盤,設(shè)甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤后指針?biāo)竻^(qū)域內(nèi)的數(shù)字為![]() ,乙轉(zhuǎn)動(dòng)轉(zhuǎn)盤后指針?biāo)竻^(qū)域內(nèi)的數(shù)字為
,乙轉(zhuǎn)動(dòng)轉(zhuǎn)盤后指針?biāo)竻^(qū)域內(nèi)的數(shù)字為![]() (當(dāng)指針在邊界上時(shí),重轉(zhuǎn)一次,直到指向一個(gè)區(qū)域?yàn)橹梗?/span>
(當(dāng)指針在邊界上時(shí),重轉(zhuǎn)一次,直到指向一個(gè)區(qū)域?yàn)橹梗?/span>
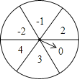
![]() 直接寫出甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤后所指區(qū)域內(nèi)的數(shù)字為負(fù)數(shù)的概率;
直接寫出甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤后所指區(qū)域內(nèi)的數(shù)字為負(fù)數(shù)的概率;
![]() 用樹狀圖或列表法,求出點(diǎn)
用樹狀圖或列表法,求出點(diǎn)![]() 落在第二象限內(nèi)的概率.
落在第二象限內(nèi)的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com