
【題目】如圖,已知平行四邊形![]() 中,
中,![]() 垂直平分線段
垂直平分線段![]() 連接
連接![]()
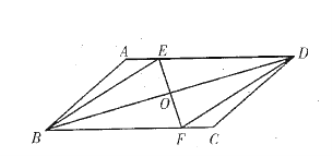
(1)求證:四邊形![]() 是菱形;
是菱形;
(2)若![]() 求
求![]() 的長.
的長.
【答案】(1)見解析;(2)1
【解析】
(1)先證明△DOE≌△BOF得到OE=OF,推出四邊形BFDE是平行四邊形,由EF⊥BD即可得到結論;
(2)過點B作BM⊥AD于M,由等腰直角三角形的性質求出BM=AM=3,再由勾股定理即可求出AE的長.
(1)∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∴∠DEF=∠BFE,∠EDB=∠FBD,
∵![]() 垂直平分線段BD,
垂直平分線段BD,
∴OB=OD,
∴△DOE≌△BOF,
∴OE=OF,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∵EF⊥BD,
∴四邊形![]() 是菱形;
是菱形;
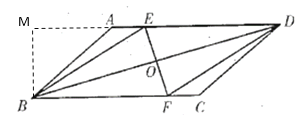
(2)如圖,過點B作BM⊥AD于M,
∵![]() ,
,
∴∠BAM=45°,
∵∠AMB=90°,![]() ,
,
∴AM=BM=3,
∵四邊形BEDF是菱形,
∴BE=DE,
∵![]() ,
,
∴![]() ,
,
∴AE=1.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=![]() ,點D是斜邊AB的中點,點E是邊AC上一點,則DE+BE的最小值為( )
,點D是斜邊AB的中點,點E是邊AC上一點,則DE+BE的最小值為( )

A. 2
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,∠B=60°,CD是⊙O的直徑,點P是CD延長線上的一點,且AP=AC.
(1)求證:PA是⊙O的切線;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足為E. 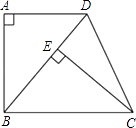
(1)求證:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
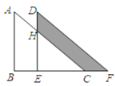
【題目】如圖,將直角三角形ABC沿著BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么圖中陰影部分的面積為____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么圖中陰影部分的面積為____ cm 2.
查看答案和解析>>
科目:初中數學 來源: 題型:
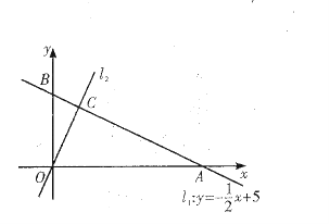
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象
的圖象![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點,正比例函數的圖象
兩點,正比例函數的圖象![]() 與
與![]() 交于點
交于點![]()
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函數![]() 的圖象為
的圖象為![]() 且
且![]() 不能圍成三角形,直接寫出
不能圍成三角形,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=5,BC=3,將矩形ABCD繞點B按順時針方向旋轉得到矩形GBEF,點A落在矩形ABCD的邊CD上,連接CE,則CE的長是 . 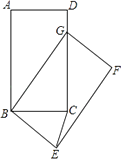
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四邊形ADEF是正方形,點B、C分別在邊AD、AF上,此時BD=CF,BD⊥CF成立.
(1)當△ABC繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,BD=CF成立嗎?若成立,請證明,若不成立,請說明理由;
(2)當△ABC繞點A逆時針旋轉45°時,如圖3,延長BD交CF于點H.
①求證:BD⊥CF;
②當AB=2,AD=3 ![]() 時,求線段DH的長.
時,求線段DH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
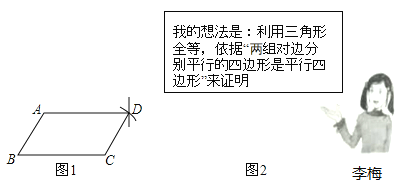
【題目】李梅同學要證明命題“兩組對邊分別相等的四邊形是平行四邊形”是正確的,她先用尺規作出了如圖1的四邊形![]() ,并寫出了如下不完整的已知和求證.
,并寫出了如下不完整的已知和求證.
已知:如圖1,在四邊形![]() 中,
中,![]() ,
,![]()
求證:四邊形![]() 是 四邊形.
是 四邊形.
(1)填空,補全已知和求證;
(2)按李梅的想法寫出證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com